Inscription / Connexion Nouveau Sujet
tg a et tg b dans systeme BAC
Bonjour à tous et toutes,
Voici un exercice qui consiste à établir le théorème des moments et à exprimer les tg a et tg β ainsi le calcule de alpha et β.
je souhaiterai svp que vous me confirmez la réponse 1 et début rép. 2.
je vus remercie par avance pour votre aide.
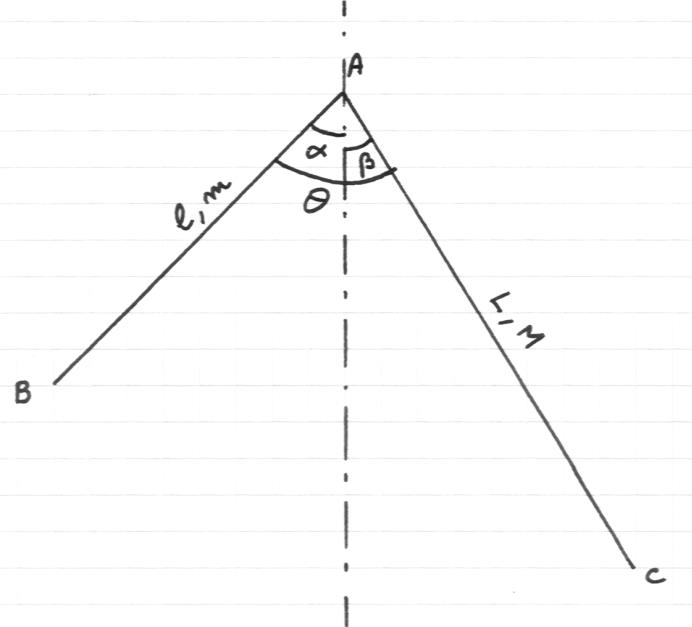
Un système BAC est formé de deux barres homogènes pesantes :
• la barre AB a pour masse m et pour longueur l ,
• la barre AC a pour masse M et pour longueur L ,
• l'angle BAC est égal à Ø
Par ailleurs, dans la position d'équilibre du système, les angles avec la verticale passant par
A des barres AB et AC sont respectivement α et β (α + β = Ø).
1- Ecrire le théorème des moments par rapport au point A.
2-Exprimer tgα et tgβ en fonction de l , L , m , M et Ø
Application numérique l = 3/5 L , M=3/5 m, Ø=90°. Calculer α et β.
1- Ecrire le théorème des moments par rapport au point A.
MA( F) = 0 soit ( L,M.g x sinβ ) + ( l,m.g x sinα) = 0
2-Exprimer tgα et tgβ en fonction de l , L , m , M et Ø
Application numérique l = 3/5 L , M=3/5 m, Ø=90°. Calculer α et β.
Tan (α)= m.g*l / FAB avec FAB la force exercée par l'axe sur la barre AB
Tan (β)= M.g*L / FAC avec FAC la force exercée par l'axe sur la barre AC
Bonjour
Attention à ton algébrisation des moments : si l'un est positif, l'autre est négatif ; cela devrait te conduire à :
La somme des deux angles vaut 90° : les deux angles sont complémentaires : le sinus de l'un est égal au cosinus de l'autre... Cela devrait facilement te conduire aux expressions des deux tangentes...
Je te laisse réfléchir et, j'espère, terminer...
merci vanoise..
vous avez tout à fait raison!..
"Si deux angles sont complémentaires , le sinus et la tangente de l'un sont égaux respectivement au cosinus et à la cotangente de l'autre " donc
tan α = cotan β
tan α = cotan ( 90° - α )
et en fonction de l , L , m , M et Ø
(Tan (α)= m.g x l x cotan β / FAB avec FAB la force exercée par l'axe sur la barre AB) mais vanoise je ne suis pas sûre du tout de ma réponse
Partant de la relation déjà écrite :
Le fait que les deux angles sont complémentaires permet d'écrire :
Si avec cela , tu n'obtiens pas les deux tangentes !
:).....Je ne sais pas ce qui m'arrive
Grosse fatigue en effet !
On retrouve au passage une propriété que tu as signalée précédemment : la tangente de l'un est égal à la cotangente de l'autre.
Annuler
connectez vous