Bonjour, je viens de faire ce QCM et j'aurai besoin de savoir si je ne me suis pas planté (et si oui, pourquoi, surtout)

L'énoncé précise que pour une grandeur sinusoïdale x(t) = 2 X cos(wt + ), avec X > 0, on associe la grandeur complexe x = X e^j

(A) La tension v(t) est donnée par l'expression v(t) = 2 Re(Zie^jwt)

On a i = Ie^ji
et v = Ve^jv
et Z = Ze^jz

v(t) = 2 V cos(wt + v)

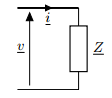
Via le schéma on a : v = i*Z
d'où V = Z*I et v =i + z

On retrouve bien l'expression du (A) donc VRAI

(B) La valeur efficace du courant est donnée par l'expression ieff = module de (v/2*Z)

v = i*Z d'où I = module de(v/Z)

FAUX

(C) La puissance active dissipée dans la charge P = module de (v²) Re(1/Z*) (le conjugué est noté Z*)

P = <v*i> = V*I*cos(z) on a I = V/Z d'où P = V²cos(z)/Z

1/Z* => module = 1/Z et = -z
Re(1/Z*) = cos(-z)/Z = cos(z)/Z

On revient au même résultat. VRAI

(D) L'argument de i par rapport à v est l'opposé de celui de Z.

Vrai, avec les mêmes équations qu'au dessus. v =i + z

(E) Si l'impédance complexe de la charge varie avec la pulsation selon la loi Z(w) = jw/(1000+jw/1000) on peut modéliser la charge par une résistance de 1k en parallèle d'une inductance de 1mH.

Z = R*jLw /(R + jLw)

Par identification => RL = 1 ; R = 1000 et L = 1mH. Ce qui est cohérent, d'où VRAI.

Qu'est-ce que vous en penser ?