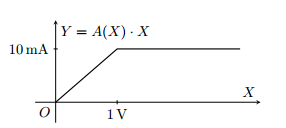Inscription / Connexion Nouveau Sujet
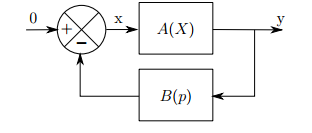
Système bouclé
Bonjour,
J'ai du mal pour répondre à une partie des questions, donc le sujet est =>
"On s'intéresse à un oscillateur quasi-sinusoïdal décrit par le schéma-bloc suivant. (voir première image)
La fonction de transfert B(p) prend la forme B(p) = R/(1 + 11RCp + 10LCp² + 10RLC²p3)
Le bloc A(X) représente un gain non-linéaire pour les oscillations. Il n'introduit pas de déphasage et la relation entre l'amplitude Y des oscillations de sortie et celle X des oscillations d'entrées est représentée par le graphe suivant : (voir seconde image)"
Les questions sont un vrai et faux.
(A) Pour réaliser le filtre B(p) il faut au moins composants de réactances non-nulle.
=> C'est vrai.
(B) La condition d'oscillation peut s'écrire -A(X)R = 1 + 11RCjw + 10LCw² + j10RLC²w3
=> Je suis parti en écrivant que B(p) = -x/y et que A(X) = y/x
d'où que B(p) = -1/A(X)
De là, j'en ai déduit que -A(X)R = 1 + 11RCp + 10LCp² + 10RLC²p3
Si on passe l'expression précédente en complexe, on se voit bien qu'on obtient pas la même. => Faux.
(C) En cas d'oscillation, la pulsation est donnée par la relation 10LCw² = 11
Je ne sais pas comment répondre à cette question.
(D) Au démarrage des oscillations le gain A(X) vaut 10m
=> A(X) = 10mA/1V = 10mS => Faux.
(E) Pour R = 1k , l'amplitude X des oscillations ne dépasse pas 1V
, l'amplitude X des oscillations ne dépasse pas 1V
=> Je ne sais pas si mon raisonnement est correcte. Pour que X < 1V, il faut qu'on soit dans la partie linéaire du Gain. Donc que A(X) = 10mS.
Si on regarde quand w = 0, au début des oscillations, on a A(X) = -1/R = 10mS.
Et si w >> 1 A(X) = j10RLC²w3/R soit un gain de 10LC²w3 et là, on ne serait plus dans la partie linéaire de la courbe. Donc...
(E) => Faux.
Voilà. Merci d'avance pour l'aide et la correction !