Inscription / Connexion Nouveau Sujet
Surface, Volume élémentaires d'un cône
Bonjour tout le monde,
Je souhaite calculer le volume et la surface latérale d'un cône de révolution en utilisant l'intégrale sur les surfaces élémentaires. Ni le système de coordonnées sphériques ni le système cartésien ne m'ont aidé. Pouvez vous me donner juste la surface latérale élémentaire ou le volume élémentaire et quel système de coordonnées avez-vous utilisé ?
Cordialement
Bonjour
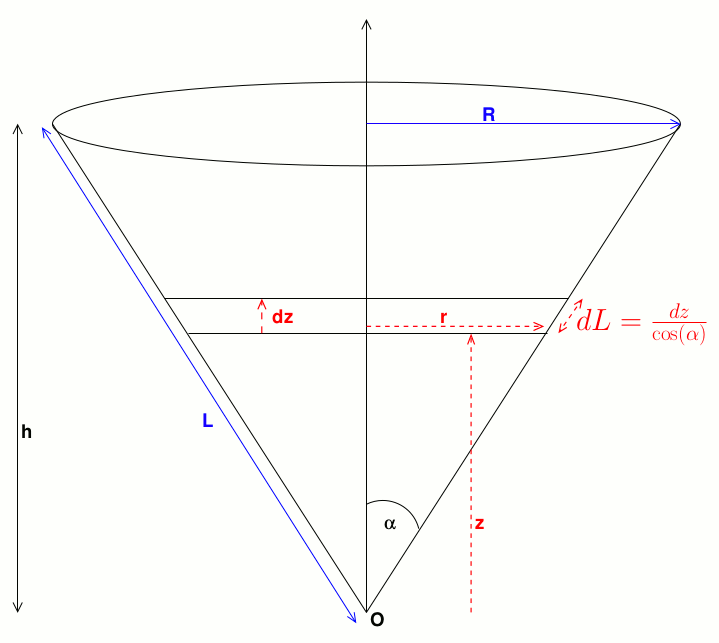
Il existe des astuces de calcul que tu peux trouver sur le net. Sinon, le système le mieux adapté est le système de coordonnées cylindriques en choisissant l'origine du repère au sommet, l'axe (Oz) étant orienté du sommet vers la base. En notant 
le demi angle au sommet, tu peux assez facilement montrer que l'aire élémentaire latérale comprise entre les plan de cotes z et (z+dz) est :
En intégrant de zéro à h : hauteur du cône, on obtient la surface lattérale :
Le rayon du disque de base est : ;
La longueur d'une génératrice est : ;
On obtient bien le résultat “classique” :
Je te laisse calculer le volume par une méthode analogue...
Bonjour,
Ni le système de coordonnées sphériques ni le système cartésien ne m'ont aidé
Et bien du coup le troisième système de coordonnées devrait être le bon.
Soit deux segments R et H perpendiculaires,
on note r un segment appartenant à R
et h un autre segment appartenant à H.
On prend finalement un segment x, tel que (r,h,x) forment un triangle rectangle en (r,h).
Maintenant, on fait varier indépendamment :
r entre 0 et R,
ainsi que h entre 0 et H.
on remarque bien que x balaie une surface, et qu'il nous suffit de sommer toutes les valeurs que prend x pour obtenir cette surface, ne resterait il plus qu'à sommer cette surface autour de son axe de rotation (H) pour avoir le volume.
Annuler
connectez vous