Inscription / Connexion Nouveau Sujet
surface elementaire d'une sphere creuse
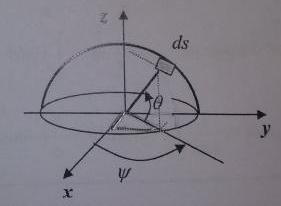
s'il vous plait je n'arrive plus à comprendre d'où vient le cos dans la surface élémentaire ds et puis dans d'autres sources je trouve l'expression avec le sin
dans la surface élémentaire ds et puis dans d'autres sources je trouve l'expression avec le sin alors je ne comprend pas qu'est ce qu'il décrit et pour quoi on l'ajoute
alors je ne comprend pas qu'est ce qu'il décrit et pour quoi on l'ajoute
** image supprimée **
je pense que la correction c'est elle qu'elle est fausse + les coordonnées de ds données sont aussi incorrectes tq:x doit être =Rcos sin
sin
y=Rsin sin
sin
z=Rcos
n'est ce pas??
x²+y²+z²=R²
x = V(x²+y²).cos( )
)
y = V(x²+y²).sin( )
)
z = R.sin( )
)
(x²+y²) + R².sin²( ) = R²
) = R²
(x²+y²) = R²(1-sin²( ))
))
(x²+y²) = R².cos²( )
)
x²/cos²(Phi) = R².cos²( )
)
x = R.cos( ).cos(
).cos( )
)
y²/sin²(Phi) = R².cos²( )
)
y = R.cos( ).sin(
).sin( )
)
---
x = R.cos( ).cos(
).cos( )
)
y = R.cos( ).sin(
).sin( )
)
z = R.sin( )
)
Sauf distraction. 
Bonjour sali17
Quand tu dois raisonner en coordonnées sphériques, il faut toujours avoir en tête l'expression du vecteur déplacement élémentaire. Si tu l'as oubliée, elle est facile à retrouver en imaginant successivement trois déplacement élémentaires :
1° : r augmente de dr à  et
et  fixe :
fixe :
2° :  augmente de d
augmente de d à r et
à r et  fixes. Le point M décrit un petit arc de cercle de rayon r :
fixes. Le point M décrit un petit arc de cercle de rayon r :
3° :  augmente de d
augmente de d à r et
à r et  fixe. Le point M décrit un petit arce de cercle de rayon r.sin(
fixe. Le point M décrit un petit arce de cercle de rayon r.sin( ) : longueur du projeté orthogonal de M sur l'axe (Oz) . Je pense que tes difficultés viennent de là !
) : longueur du projeté orthogonal de M sur l'axe (Oz) . Je pense que tes difficultés viennent de là !
L'aire d'une surface élémentaire à la surface de la sphère de rayon R correspond au produit des deux déplacement élémentaires suivant Ur et U à r=R fixe.
à r=R fixe.
Tu pourrais aussi déduire de ces déplacement élémentaires le volume élémentaire exprimé en coordonnées sphériques : c'est le produit des trois déplacement élémentaires :
Avec tout cela, tu pourrais t'entraîner à retrouver les expressions de l'aire de la surface d'une sphère de rayon R et le volume d'une boule de rayon R.
vanoise oui quand je fait mon raisonnement je trouve dS=R^{2}.d\psi.\sin\left(\theta\right).d\theta aussi,alors y'a rien que cette réponse et je peux considérer la correction de cet exercice fausse!!?
Désolé : l'habitude est de considérer pour angle  , le complémentaire de celui de ta figure d'où l'erreur que j'ai commise entre cosinus et sinus. Je rectifie :
, le complémentaire de celui de ta figure d'où l'erreur que j'ai commise entre cosinus et sinus. Je rectifie :
La notation la plus fréquente pour les coordonnées sphérique est celle de la figure ci-dessous.
La force de l'habitude... Désolé !
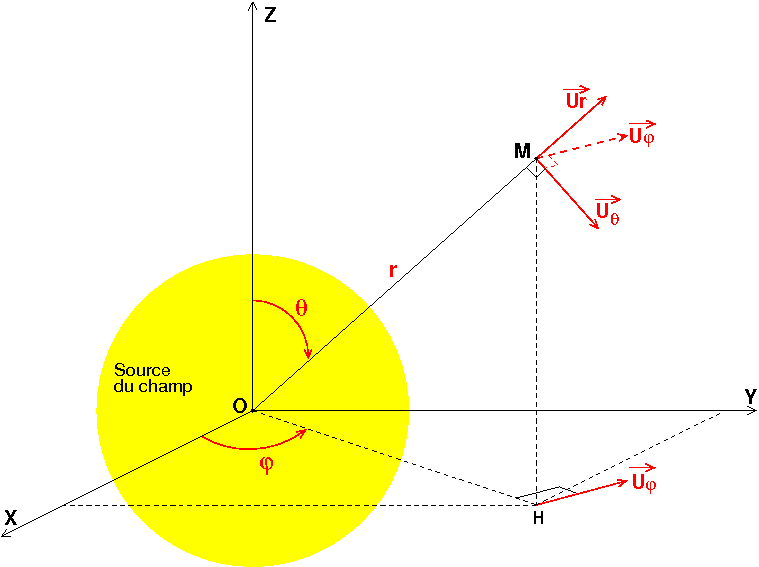
Habituellement, on prend ceci :
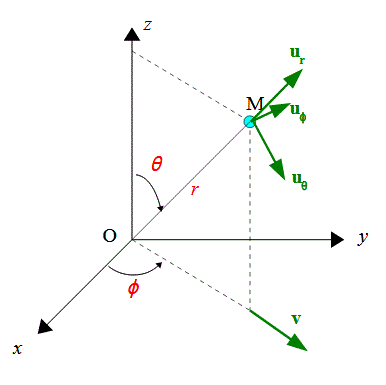
Mais dans le dessin que tu as donné, l'angle theta indiqué n'est pas le même.


 :?
:?
