Hello

Ton questionnement a le (seul?) mérite d'être original mais ne pose aucune réelle question en rapport avec la physique ou la chimie.  Je crois être avec accord avec le projet de ce forum en te posant en retour 2 questions:

- quels éléments souhaites tu vérifier?
- quelles sont les questions sur lesquelles tu butes?

Bonsoir Dirac,

Je m'excuse de ne pas avoir réellement posé une question en rapport avec de la physique mais le sujet corrigé que j'aimerais avoir est bel et bien en rapport avec de la physique. Il s'agit d'un sujet qui traite des forces appliquées sur une balançoire mais bien que connaissant mon cours, certaines questions ( nombreuses tout de même pour les citer) restent floues a mes yeux. C'est pour cela que je voulais savoir si quelqu'un ayant accès aux corrigés de concours pouvait me donner celui correspondant au sujet que j'ai fait.
De plus j'ai posé la question sur ce forum car je pensais qu'il serait le mieux pour avoir des réponses sérieuses de personnes bienveillantes ^^

Hello

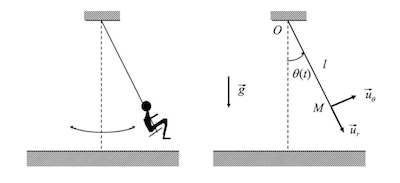
Un enfant faisant de la balançoire est modélisé par une masse ponctuelle m située en M et suspendue en O par un tige rigide, de masse négligeable et de longueur l.

L'angle que fait la tige avec la verticale orientée vers le bas est noté

Le repère orthonormé lié à la balançoire est noté  

Schéma fourni dans l'énoncé ci dessous

1) A quelle condition sur la durée de l'expérience, le référentiel terrestre peut il être considéré comme galiléen ? (on donnera un ordre de grandeur)

durée << 24h

2) Etablir l'équation différentielle du mouvement en utilisant la RFD :



Soit, en projetant sur :  

Donc :  

3) Etablir l'équation différentielle du mouvement en utilisant le théorème de l'énergie cinétique :

La variation d'énergie cinétique est égale au  travail du poids



Soit en dérivant par rapport au temps, on retrouve :

4) Etablir l'équation différentielle du mouvement en utilisant le théorème du moment cinétique :



Soit

Et donc une nouvelle fois :

5) En déduire que le mouvement est plan :

Cette question est un peu surprenante car l'énoncé, bien que ne précisant pas les conditions initiales, le laisse entendre. On imagine mal dans ce dispositif un mouvement de translation le long de l'axe Oz

6) A quelle condition l'enfant assis sur la balançoire sera-t-il un oscillateur harmonique?

L'équation caractéristique d'un oscillateur harmonique est   où   est sa pulsation propre

La condition est donc ici   soit (2nd terme du DL de la fonction sinus négligeable devant le premier)  

7) Donner l'expression littérale de la pulsation

L'équation du mouvement de M est : donc par identification

8) L'enfant part d'un angle   sans vitesse initiale. Avec les valeurs numériques suivantes : et calculer la période de l'oscillateur harmonique, ainsi que la vitesse maximale de l'enfant.



La vitesse maximale est atteinte en où  

Soit


9) En partant de la réponse à la question 3) exprimer en fonction de et des caractéristiques du système. En déduire la période sous forme d'une intégrale en fonction de et des caractéristiques du système (On précisera soigneusement les bornes d'intégration. On ne demande pas de calculer cette intégrale) :

Nous avions :  



Avec

Donc,  



Retrouver le résultat de la question 8) dans le cas des petites oscillations :
Le DL à l'ordre 2 de la fonction cosinus est
Ce qui donne, en posant

On reconnaît la dérivée de la fonction Arcinus
Donc    (avec  pour rappel :  )

Est ce qu'arrivés là nous sommes d'accord?

En poursuivant la résolution du problème, je tombe sur une coquille dans ce que j'ai écris ce matin:

Dans la question 8) concernant la détermination de

J'ai écris:    

Il fallait lire (enfin ... j'aurais du écrire):    

Ce qui nous amène à  

Soit numériquement

Arrivé là on se dit que:

1) l'usage de la calculette n'est pas autorisé et qu'il faut fait le calcul de
2) qu'en utilisant le théorème de l'énergie cinétique et son expression établie en début de problème, on n'utilise pas le fait que l'on s'est placé dans le contexte d'un oscillateur harmonique.

Faisons le donc:



Soit  

Soit  

est obtenu pour

Donc  

Soit numériquement:  

La suite ... (mais pas la fin)


10) Une intégration numérique permet de dessiner la courbe représentative de la fonction ci- dessous. Commenter cette courbe.

Cette question fait référence à l'expression « exacte » de T :  

- On retrouve bien la valeur de 3,1 s pour les valeurs de au voisinage de 0
- Pour les petites valeurs de   (inférieures à ) la dépendance de T à reste très faible
- Ensuite, l'approximation n'est plus acceptable, l'accélération dûe à la pesanteur variant en est moins importante que celle du modèle, la période d'oscillation s'allonge.

Là encore, le sujet est un peu déroutant car proposer des valeurs de supérieures à 90° pour un départ arrêté de l'enfant n'a pas vraiment de sens.

11) Etablir cette fois l'équation différentielle du mouvement en faisant un DL à l'ordre 3 de la fonction sinus



L'équation devient donc :  

12) On cherche, pour l'équation différentielle approchée écrite en 11), une solution elle-même approchée de la forme :

  avec  
Exprimer, en se limitant au premier ordre en , les valeurs de et de  

En utilsant la forme de



En faisant également un DL à l'ordre 1 de :



L'équation différentielle s'écrit alors :



Arrivé là on se dit que l'énoncé qui demandait un DL à l'ordre 1 en ne devait pas se dispenser de réfléchir !

Les termes en peuvent être négligés devant les termes en et les termes en , l'équation devient alors (et c'est tant mieux) :



Cette équation est vérifiée à chaque instant dès lors que :

, Soit  

Et que :, Soit


13) Par rapport au mouvement harmonique, la courbe relative au mouvement réel a-t-elle une plus grande ou une plus petite période ?


(Tout ça pour cette question ? )

  donc   donc

Comme attendu, la période du mouvement « réel » est plus grande que celle de l'oscillateur harmonique.

14) Quelle est la pulsation du premier harmonique après le fondamental ?

Le mode fondamental () a pour amplitude

Le 1er harmonique à a une amplitude de

(On a vu apparaître un 2nd harmonique à d'ailleurs)

15) Dans le cas général où on ne se limiterait pas à des développements au premier ordre, quelle serait l'allure du spectre de la solution obtenu par analyse spectrale ?

La décomposition en série entière de la fonction se décompose en puissances impaires de
s'écrit comme polynome de puissances impaires de
Le spectre de la solution réelle est une somme d'harmoniques impaires, d'amplitudes décroissantes

Arrivé là, on a du faire 40% du sujet. On continue?

16) Au point O s'exercent des forces de frottement sur la tige. Le moment de ces forces par rapport à O est égal à , où C est une constant positive.  Quelle est la dimension de C ?

  Donc

17) Etablir l'équation à laquelle doit maintenant obéir

Il suffit de compléter l'expression issue du théorème du moment cinétique établie en 4)



Soit

18) En supposant que l'angle reste suffisamment petit, à quelle inégalité doit satisfaire C pour que le mouvement de l'enfant puisse être considéré comme un mouvement oscillatoire dont l'amplitude décroît avec le temps (mouvement pseudo-périodique) ?



L'équation devient



Equation différentielle dont l'équation caractéristique est :



Le mouvement sera oscillatoire amorti dans le cas où le discriminant de cette équation est négatif strictement :

Soit   et donc    ou bien    (avec )

Le facteur d'amortissement exponentiel est :  

La pulsation est :  

19) Application numérique : considérant cette condition satisfaite, on approxime ici la pseudo-période à la période de la question 8). L'enfant part d'un angle sans vitesse initiale. On observe que l'amplitude du mouvement est réduite de moitié après 20 oscillations. Calculer la valeur de la constante C avec les valeurs numériques fournies.

Donc

Et pour , Soit  

Et finalement :  

(Comme calculette pas autorisée, )

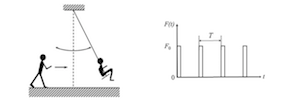
Les frottements ont pour conséquence d'amortir le balancement de l'enfant et un deuxième enfant vient donc aider le premier enfant qui se balance à maintenir une amplitude constante en le poussant avec une force horizontale périodique non harmonique dont le module F(t) est représenté ci dessous.

20) A quel moment et à quelle fréquence l'enfant pousseur doit-il appliquer sa poussée sur l'enfant de la balançoire pour que son action soit la plus efficace possible ? Que vaut donc la période T de la force F(t) pour que l'action de l'enfant pousseur soit la plus efficace possible ? (on supposera les frottements faibles dans cette question et dans les suivantes).

Par « le plus efficace possible » on entend certainement que la force appliquée pendant chaque (bref) intervalle de poussée transfère le maximum d'énergie à la balançoire pour des valeurs de et de données.



La force ayant, précise l'énnoncé, une direction horizontale :



Or est maximale en   aux instants

A noter que lorsque est maximale, la force de frottement de l'axe rigide l'est également. Mais les l'énoncé précise que ce frottement est faible, et n'intervient donc pas dans l'évaluation de l'efficacité de la poussée.

correspondant également au maximum de la fonction cosinus.
Donc la poussée la plus efficace sera effectuée :

- A la fréquence   (dont la valeur numérique sera confondue avec )

- A chaque passage, orienté vers l'avant, à la verticale de O

21) Déterminer la puissance moyenne dissipée par les frottements en fonction de C, la pulsation du mouvement et l'amplitude du mouvement. En déduire le travail fourni par l'enfant pousseur après 20 oscillations



Donc   avec  

Donc

Sur 20 oscillations l'enfant pousseur fournit le travail :



Numériquement:  

Hello

Pendant que VINCENZ0O potasse le sujet (de tte façon j'ai encore une 15zaine de questions à traiter, je m'y colle dès que j'ai un peu -plus- de temps ...), je fais écho à une remarque de vanoise qui très amicalement souligne que j'avais "bâclé" la réponse à la première question (Je crois qu'en conditions "réelles" je l'aurais effectivement bâclé dans un premier temps pour y revenir dans un second: le sujet n'étant pas vraiment interessant -au moins pour ce que j'en ai vu- sur le plan de la réflexion pratique mais plutôt un long enchainement de calculs avec qlq chausse-trapes) donc à la réflexion et s'agissant d'une épreuve pour des écoles d'ingénieur: démontrer que l'on a un sens "physique" est sans doute de nature à plaire aux correcteurs:

La question posée était:
A quelle condition sur la durée de l'expérience, le référentiel terrestre peut il être considéré comme galiléen ? (on donnera un ordre de grandeur)

Le référentiel terrestre étant lié au sol, on pourra le considérer comme galiléen tant que les effets de la rotation de la Terre peuvent être négligés.

Un point fixe au sol décrit un arc de cercle dont le rayon est fonction de la latitude.  

Durant un intervalle le point parcourt:

- un arc de longueur s

- dont la corde est

On doit pouvoir confondre les 2, c'est à dire considérer un intervalle suffisamment petit pour que

en faisant un développement limité à l'ordre 3 de la fonction sinus on obtient



On veut donc:    Soit

Une durée d'expérience de l'ordre de 30 mn me semble donc très raisonnable.

NB:
Lorsque l'on écrit "les effets de la rotation de la Terre peuvent être négligés" on est tenté je crois de faire référence à la force de Coriolis (la force centrifuge étant comprise dans le poids), sauf qu'alors je ne vois pas de chemin rapide pour justifier un ordre de grandeur sur la durée

NB2: en confondant arc et corde je confonds le mvt du référentiel terrestre  par rapport au référentiel géocentrique avec un mvt rectiligne (uniforme) et donc je peux le qualifier d'inertiel (ça va peut être encore mieux en le disant )  

Bonjour dirac
Tu as raison de te montrer assez critique concernant l'énoncé. D'ailleurs ce sujet avait soulevé de vives protestations de la part des professeurs de CPGE lors de sa sortie.
Je me demande si le concepteur de l'énoncé n'attendait pas à cette question une simple réponse qualitative du type : "la durée de l'expérience doit être très courte devant la période T_F de rotation du plan d'oscillation du pendule avec :


avec : : latitude du lieu de l'expérience.
J : durée d'un jour stellaire : 86164s"
Sous toutes réserves évidemment...

Hello vanoise,

Peut être ... ci dessous ce que je viens de glaner sur le site du concours dans le rapport de l'épreuve 2013:

La grande majorité des réponses sont bien argumentées, mais une partie reste vague où des grandeurs sont données sans dire par rapport à quoi elles sont comparées. La principale erreur réside dans la confusion entre référentiel terrestre et référentiel géocentrique (bien distinguer la rotation propre de la Terre de sa rotation autour du Soleil). Enfin, beaucoup de candidats se contentent de dire que la durée de l'expérience doit être très inférieure à 24 h mais ne donnent pas un ordre de grandeur comme demandé par l'énoncé.

Pour l'ordre de grandeur, une idée possible :
on peut considérer comme  négligeable une rotation du plan de rotation inférieure au degré. Cela conduit, à la latitude de 45° à une durée t telle que :


De toutes façons, tout cela est très formel . Sans prendre les précautions expérimentales propres à la réalisation d'un pendule de Foucault, les frottements amortissent le mouvement et le pendule finit par s'immobiliser bien avant qu'une quelconque rotation du plan d'oscillation ait pu être mesuré !
Le choix d'une rotation inférieure au degré est tout a fait arbitraire...

Retour sur le sujet:

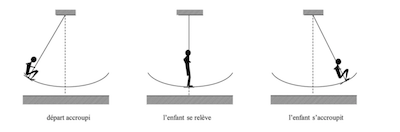
22) L'enfant se balançant décide de monter sur une autre balançoire, pour laquelle les frottements sont considérés comme totalement négligeables. Alors que l'enfant se balance, il décide de monter de plus en plus haut. Pour cela, il effectue les mouvements suivants au cours des phases oscillatoires successives, 1, 2, … (voir schémas)

Dans un repère lié à la balançoire, identifier les forces extérieures au système :

(encore un passage où la formulation est un peu « perturbante »)

La réaction de l'axe de la balançoire, qui s'applique en 0 :



Le poids du dispositif (l'énoncé n'en disant rien de particulier, on suppose que la masse se concentre au moint M) :



Les forces d'inertie : si par repère le rédacteur avait en tête référentiel, il faudra aussi considérer les forces d'intertie d'entrainement mais aussi de Coriolis l'enfant étant en mouvement dans ce référentiel.

Il n'y a plus que moi qui suis ce sujet ... VINCENZ0O étant parti en vacances? Je comptais bien l'avancer aujourd'hui et finalement je n'avance que 5 questions (il en restera une 12aine):

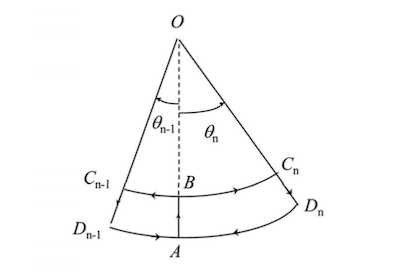
23) Evaluer alors dans ce même repère lié à la balançoire, pour chacune des forces extérieures au système, le signe du travail qu'elles produisent sur un demi-cycle ABCnDnA.

Le point M étant immobile dans le référentiel balançoire durant les portions B,Cn et Dn,A du trajet, seules les portions A,B et Cn,Dn sont à considérer.

Par ailleurs :
- R ne travaille jamais sur aucune des portions du trajet (exercée en O)
- La force de Coriolis ne travaille jamais non plus : car perpendiculaire au déplacement sur A,B et Cn,Dn

Enfin, un déplacement élémentaire sera colinéaire à sur les portions A,B (sens opposé) et Cn,Dn (même sens)

Considérons donc 2 déplacements -dl et +dl effectués par M pour une même valeur d'abscisse sur la droite :

Sur A,B (-dl) :



Sur Cn,Dn :



Donc :



Avec atteignant son maximum pour
Et pour

Donc :

Le travail des forces extérieures (poids est inertie) est donc résistant.

24) En appliquant alors le théorème de l'énergie cinétique sur le demi-cycle ABCnDnA, en déduire que le travail des forces intérieures dû au mouvement du corps de l'enfant, qui se relève et s'accroupit, est de signe positif

Là encore l'énoncé ne me semble pas optimal, non pas que le théorème de l'énergie cinétique appliqué dans ce référentiel non galiléen pose problème, mais le rédacteur considère comme « acquis » que le mouvement A,B lorsque l'on vient de Dn est le même que celui de Dn-1.

Faisons donc cette hypothèse : alors sur un ½ cycle

Donc   Soit  

25) Il est rappelé que pour tout système de points matériels, le travail des forces intérieures se conserve dans un changement de référentiel (il n'est pas demandé de démontrer cette propriété). En appliquant le théorème de l'énergie cinétique dans le référentiel galiléen lié au sol, en déduire que le mouvement du corps de l'enfant, qui se relève et s'accroupit, permet à la balançoire de monter de plus en plus haut.

Au cours d'un cycle, dans le référentiel galiléen (lié au sol) :



Or    (c'est l énoncé qui nous le dit)

Et  , car les frottements étant négligeable (c'est encore l'énoncé qui nous le dit), le poids est une force conservative et la réaction de l'axe ne travaille pas

Donc

A chaque au point A l'enfant possède une énergie cinétique supérieure à celle du cycle précédent, cette énergie se transformant en énergie potentielle (proportionnelle à la hauteur maximale atteinte).

A chaque cycle l'enfant ira de plus en plus haut.

26) Modélisation simplifiée de la balançoire et de l'enfant.
On schématise la balançoire et l'enfant comme un pendule de masse fictive (constante) m accrochée à un fil de longueur variable dépendant de la position angulaire de repérage : . Calculer le moment cinétique, LO , du pendule au point O dans le référentiel galiléen lié au sol.

Ce que nous avions noté OM jusqu'à présent sera désormais noté l



Soit

27) En appliquant le théorème du moment cinétique dans le référentiel galiléen lié au sol, donner l'équation vérifiée par LO .


En se souvenant de ce qui a été fait à la question 4)




A suivre ...

Bon,  on avance:

28) Montrer que (écartements maximaux) vérifient la relation :



L'énoncé suggère d'effectuer:



Soit

Donc  

Soit

Avec

Donc

A noter que le fait référence au fait que représente une amplitude et non pas une valeur algébrique, comme le laisse entendre la figure (voir plus haut) de l'énoncé. De mon point de vue il est toujours plus prudent d'embarquer un sens de rotation positif par le choix d'un repère puis d'utiliser exclusivement des valeurs algébriques, mais bon …

29) Montrer que les positions angulaires extrêmales successives, et , obéissent à une loi de récurrence faisant intervenir et .
On prendra   pour et pour .

Plus encore que les coquilles précédentes sur « repère » employé à la place de « référentiel », le choix de l'indexation (par ½ cycle) et de l'utilisation d'amplitude plutôt que de valeur algébrique a dû laissé qlq candidats un peu perplexes

La portion de trajet que nous étudions dans cette question est uniquement le ½ cycle  Dn,A,B,Cn+1 qui lorsque l'on passe à l'indice suivant nécessite un x(-1) sur la valeur de .

On a donc :



Soit



Soit



Arrivé là l'énoncé demande d'établir une relation en et . Cela n'apporte rien et en avançant les questions suivantes, on se dit qu'il s'agit d'une nouvelle coquille : le rédacteur aurait mis les candidats sur de meilleurs rails en demandant d'établir une relation en ) et

Car alors la relation précédente devient immédiatement



30 ) En déduire les valeurs des positions angulaires extrémales atteintes par l'enfant sur sa balançoire

L'expression précédente caractérise une suite géométrique de raison

Donc
(l ‘énoncé indiquant que la première oscillation porte l'indice 1, bien que dans la dernière partie du problème il soit fait référence à un \theta_0)

31) Si l'enfant démarre sans vitesse initiale, quelle est la position la plus avantageuse pour démarrer ? La balançoire pourrait-elle faire accomplir un tour complet autour de son axe de rotation ( « grand soleil » comme à la barre fixe) ?

La position la plus avantageuse correspond(rait) à (mais là, le garnement n'est plus sur une balançoire mais dans une école de cirque !)

L'enfant apportant de l'énergie cinétique au système à chaque cycle, il vient nécessairement un moment où il arrive en avec une Energie cinétique non nulle et fait alors un grand soleil.

32) Une autre manière de faire monter sa balançoire est la suivante : l'enfant peut rester assis et mettre son dos alternativement en avant ou en arrière tout en repliant puis étendant ses jambes afin de faire lever ou abaisser son centre de gravité.
En supposant comme précédemment que la masse de la balançoire est négligeable, on modélise la balançoire et l'enfant comme un ensemble de deux masses articulées. La masse totale de l'enfant est en notant m la masse du corps en M (la longueur de la balançoire OM est L) et la masse des jambes (la distance entre le centre de masse des jambes A - qui est situé environ à la position des genoux - et le point M est AM = a comme indiqué sur la figure ).

A la montée, l'enfant met et maintient ses jambes en « avant » tandis qu'à la descente l'enfant met et maintient ses jambes « en arrière ». Pour simplifier, il est supposé que la direction AM fait un angle droit avec la direction OM à la montée comme à la descente
Calculer le moment cinétique de l'enfant, LO , au point O dans le référentiel galiléen lié au sol



Soit


33) Calculer le moment des forces de pesanteur par rapport à l'axe Oz, dans le cas où  la balançoire est dans une phase de montée et dans le cas où la balançoire est dans une phase de descente. On pourra introduire l'angle tel que



A la montée

A la descente

Donc :

- Cas montée :



- Cas descente :



34) En appliquant le théorème du moment cinétique, établir les équations du mouvement :

En écrivant que \, on obtient :

Cas montée :



Soit

Avec

Et

Cas descente :



35) Dans le cas de petites oscillations, donner les équations linéarisées du mouvement à la montée et à la descente.


On fait les approximations suivantes   et

Cas descente :



Cas montée :



36) Montrer que le mouvement est l'analogue d'un oscillateur harmonique excité dont on donnera la pulsation propre et la fonction excitatrice

En lisant cela, on comprend qu'il est attendu également un DL d'ordre 1 en \phi (ce qui à la réflexion est raisonnable lorsque l'on va en fin d'énoncé regarder l'application numérique demandée)

Les conditions initiales associées à cette question étant :, à t = 0   et « jambes en avant ». Ce qui est très étrange car dans ces conditions
A , l'enfant commence à descendre et il est dit un peu plus tôt dans l'énoncé qu'à la descente, l'enfant avait les jambes en arrière

Cas descente :



Cas montée :



Les équations ci dessus sont bien celles d'un oscillateur harmonique de pulsation :



(on est rassuré que la pulsation propre soit celle attendue)

Et excité par une fonction telle que :
sur
sur
sur
sur

Il s'agit donc d'une fonction créneau dont la fréquence est double de celle de l'oscillateur harmonique  

Soit

  pour

pour

Avec

37) Décomposer la fonction excitatrice en série de Fourier.  D'après le rappel fait en début d'énoncé sur les décompositions en série de Fourier :



Avec





Et là nouveau stop, car je ne trouve pas ce que l'énoncé demande d'établir. A suivre ... (plus que 4 questions )

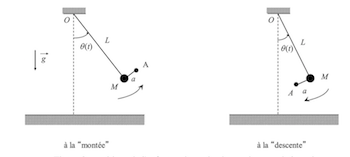
Je viens de comprendre! quand le rédacteur écrit "à la descente" il veut dire l'enfant va vers l'avant (de gauche à droite), même si pendant la moitié de ce trajet ... il monte.
Même confusion sur le terme "à la montée".

Si cet énoncé  était pensé avec l'objectif de préparer les futurs ingés à la vraie vie: expression de besoins incorrects, cahier des charges bourrés de coquilles, textes réglementaires incohérents ... Objectif atteint! Je crois que j'aurais été sérieusement "perturbé" lors de cet écrit

Les 4 questions finales n'apportant pas grand chose de nouveau, si Vincenz0o (ou un autre) souhaite creuser on creusera, mais pour le moment j'en reste là

Bonjour dirac
Tout d'abord : bravo pour cet énorme travail ! J'espère que Vincenzoo l'appréciera à sa juste valeur mais çà : ce n'est pas gagné !
Je partage ton point de vue sur l'énoncé : la dernière partie en particulier. L'énoncé semble un peu s'inspirer de problèmes anciens sur la résonance paramétrique et le fameux "botafumeiro" de Saint jacques de Compostelle mais la méthode de résolution proposée est inutilement compliquée et pas du tout adaptée au profil de l'étudiant moyen susceptible d'intégrer les C.C.P... Les nouveaux programmes demandent davantage de raisonnement physique et moins de calculs...
A mon avis, le changement de référentiel proposé est sans intérêt ; un simple raisonnement sur l'énergie mécanique du système {balançoire - enfant}, mesurée dans le référentiel terrestre, suffit. Si on note "b" l'augmentation d'altitude du centre de gravité de l'enfant de masse "m" quand il se met debout en passant à la verticale, il suffit de remarquer que l'énergie mécanique du système augmente alors de "m.g.b" alors que, lorsqu'il se remet assis en =_m, le système perd l'énergie "m.g.b.cos(_m) ; il y a bien augmentation de l'énergie mécanique du système. L'énoncé peut alors guider l'étudiant pour obtenir l'augmentation d'amplitude des oscillations...
Bravo encore !

merci vanoise. Mais le mérite n'est que celui de l'âne qui accepte de porter un bât! Ce sujet n'ayant comme tu le soulignes aucun intérêt en ce qui concerne la résolution pratique d'un problème physique réel. Contrairement à la grande majorité (il me semble) des sujets proposés aux concours d'entrée aux Grandes Ecoles / écoles d'ingénieurs.