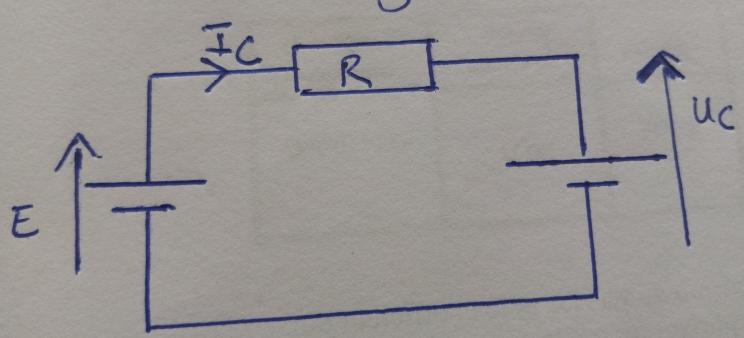
Bonjour,

Pour mémoire :

extrait de la FAQ du forum :

Q01 - Que dois-je faire avant de poster une question ?

Plusieurs choses sont à faire avant d'envisager de poser une question sur le forum.

Tout d'abord, réellement chercher à résoudre seul votre problème. En effet, le but du forum n'est pas de faire les exercices à votre place.

Cherchez également si votre question n'a pas déjà été posée sur le forum. Pour cela vous pouvez utiliser le moteur de recherche (en panne pour le moment) ou le net en tapant quelques mots clés, par exemple, le début de votre énoncé.

Vous pouvez aussi parcourir le forum en choisissant une classe spécifique (de la sixième au supérieur) dans la page de choix du forum. Vous trouverez certainement un exercice déjà posté et corrigé qui ressemblera fortement au vôtre.

Enfin, vous pouvez également consulter les fiches du site se rapportant à votre chapitre. Parfois une simple relecture de celles-ci vous permettra de vous rappeler d'une définition, d'une propriété, d'une condition d'application d'une loi (données, hypothèses, ...), d'une méthode oubliée, etc.

Somme toute, n'envoyez pas le sujet d'un exercice sans montrer que vous y avez travaillé sérieusement.

Condensateurs et dipôles RC

Oui mais bon je comprend pas trop le sujet essayez de m'aider à le traiter svp.

Ce que tu nous demandes c'est de faire l'exercice à ta place et il en est hors de question en vertu des règles de ce forum.

Je t'ai fourni la fiche de cours qui t'explique comment le résoudre, la balle est dans ton camp désormais : si tu souhaites partager tes réflexions, je les regarderai, sinon, l'échange s'arrêtera malheureusement là ...

Ok d'accord je vais essayer de faire ce que je connais et vous faire part

ça marche, donne-toi le temps de l'étude de cette fiche, on l'a remise à jour il y a peu, elle est complète.

Je regarderai ce que tu as fait en fin de journée ou au plus tard demain matin

D'accord pas de soucis merci m'sieur

1) d'après la loi des mailles
Uc+R+Ic-E=0
Uc= R.E x Ic

2) équation différentielle de q(t)
Le condensateur c est initialement déchargé :
Selon la loi des mailles: Uc+R+Ic-E=0

Ur= R. d(C.Uc)/dt ≈ Ur = R.C. dUc/dt
RC.dUc/dt+ Uc=0
Équation différentielle : dUc/dt + Uc/RC =0.

4) déduisons les expressions de Uc(t) et Ic(t):

Uc(t)= E.e(-t/RC)
Ic(t) = -E/R . e(-t/RC)

J'AI PAS FAIT LA QUESTION (3)

1. Ça commence déjà mal : la loi des mailles concerne une somme de tensions aux bornes des dipôles d'une maille ; or ici tu mélanges des tensions et une intensité du courant.

Si tu as des doutes, relis les bases ici : Signaux et circuits électriques complexes : les capteurs

Ok d'accord

Bonsoir,

Tu t'en es sorti ?