Inscription / Connexion Nouveau Sujet
structure iso RDM
Bonjour,
J'ai un soucis dans mon exercice de RDM pour trouver les réactions d'appuis, car la géométrie de la structure m'embrouille pour écrire les équations du moment statique en D, puis le moment en B et E, nul comme rotule.
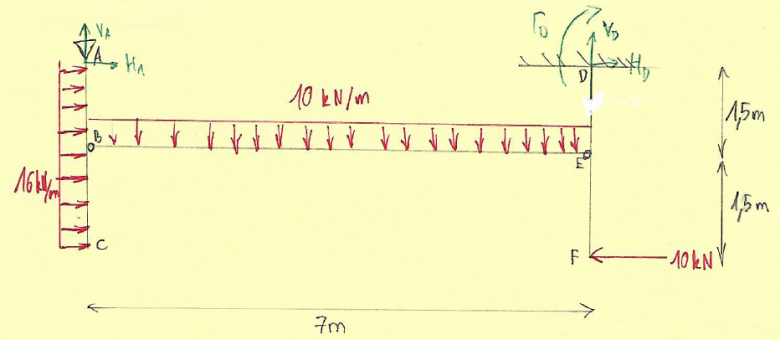
merci de bien vouloir m'aider pour ces équations
j'ai deja les deux simples:
Bonsoir,
Ta poutre a bien un profil en I, encastré en D et appui simple en A ?
Ensuite, as-tu vérifié si elle est bien isostatique ?

Dans ce cas, il faut jouer sur les "zéros" des liaisons, de manière à supprimer des inconnues dans ton équation.
Par exemple une équation de moment en D pourrait faire l'affaire, également en A.

Oui c'est bien ce que j'ai précisé.
Il faut une équation de moment statique en A ou en D au choix.
Et il en faut deux autres pour les rotules en B et en E. Mais cette fois ce sont des moments en un point qui sont calculés et non plus un moment global comme précédemment.
C'est cette démarche (avec les coupures notamment) que je n'arrive pas à mettre en œuvre
Pardon, je n'avais pas compris la présence d'une rotule en B et E.
Etant donné qu'elle supprime 1 DDL, tu as deux actions à prendre en compte en plus par rotule :
Vb et Hb
Ve et He

Avec les indications que tu m'as données ne parvient toujours pas à trouver les équations de moment écrites aux points rotules.
Moment = effort x bras de levier, le signe dépendant du "sens" vis-vis du repère.
Equation du moment statique en B / axe z (perpendiculaire à ton schéma, dirigé vers toi) :
-1,5*Ha + 0 (contribution nulle de Va) + 0 (contribution nulle de l'effort équivalent 3*16) - 3,5*(7*10) + 7*Vd - 1,5*Hd + 7*Vd -1,5*10 + moment en D + 7*Ve = 0
Sauf erreur d'inattention, en application du théorème de BABAR.
En revanche, je ne te cache pas que je suis surpris qu'on te donne un tel exercice en math spé ...
Un système que tu dis isostatique avec 9 inconnues, ça signifie devoir trouver 9 équations ...
Moment = effort x bras de levier, le signe dépendant du "sens" vis-vis du repère.
Equation du moment statique en B / axe z (perpendiculaire à ton schéma, dirigé vers toi) :
-1,5*Ha + 0 (contribution nulle de Va) + 0 (contribution nulle de l'effort équivalent 3*16) - 3,5*(7*10) + 7*Vd - 1,5*Hd + 7*Vd -1,5*10 + moment en D + 7*Ve = 0
Merci c'est exactement ça qui me fallait.
En revanche, je ne te cache pas que je suis surpris qu'on te donne un tel exercice en math spé ...
Ce n'est pas le cas, je suis en école, mais j'ai le niveau mathspé alors je prefere indiquer sur le niveau de l'exercice mon niveau perso que le niveau de l'exo pour le pas etre perdu.
Un système que tu dis isostatique avec 9 inconnues, ça signifie devoir trouver 9 équations ...
Comment ça 9 inconnues, il n'y a que 5 réactions d'appui donc 5 inconnues


