Niveau école ingénieur

Structure Dynamique

Posté par
speed 14-05-17 à 17:32

Bonjour,

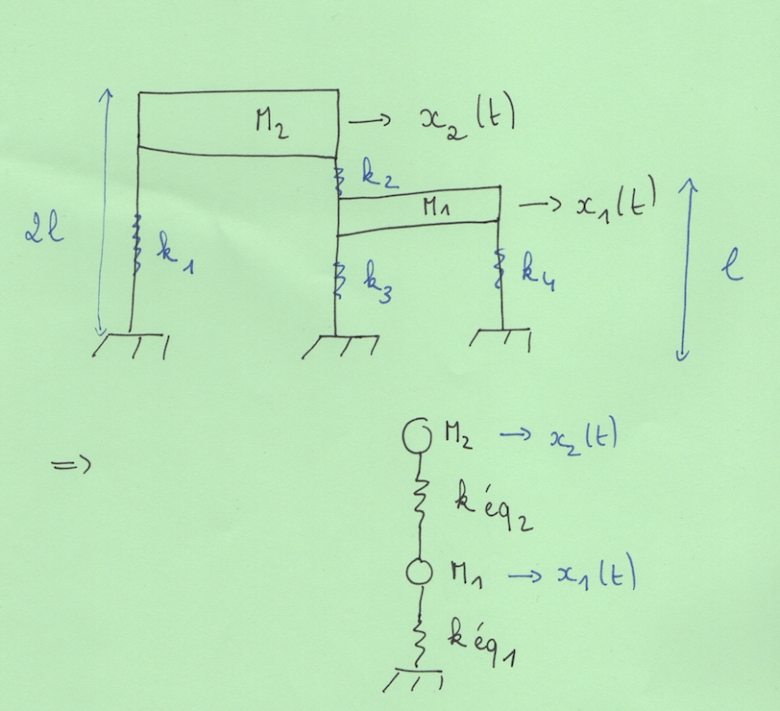
Voilà j'ai un exercice d'analyse de la dynamique d'une structure (cf image) je l'ai modélisé comme un oscillateur.

J'ai d'abord calculé les différents ki (raideur des ressorts).

k1=12EI/(8l^3)
k2=12EI/(l^3)
k3=12EI/(l^3)=k4

Mon problème c'est le calcul des kéquivalents :

Je ne sais pas si c'est correcte

keq1=k1+k3+k4

keq2=k1+k2

Structure Dynamique

Posté par re : Structure Dynamique 14-05-17 à 17:33

Je vous remercie pour votre aide

Posté par re : Structure Dynamique 14-05-17 à 17:44

Bonjour
Les raideurs équivalentes pour les ressorts se calculent comme les capacités équivalente des condensateurs : ressorts en parallèle comme le 3 et le 4 : les raideurs s'ajoutent ; ressorts en série (bout à bout) : les inverses des raideurs s'ajoutent...
Les choses ne sont pas tout à fait aussi simples...
Si, comme cela est précisé : k3=k4, le solide de masse M1 ne restera pas horizontal au cours des oscillations si l'action de k2 ne s'exerce pas à la verticale du centre de gravité du solide de masse M2.
Il faut ensuite trouver une relation entre k1, k2 et (k3+k4) pour que le solide de masse M1 oscille en restant horizontal...

Posté par re : Structure Dynamique 14-05-17 à 18:00

Pour la masse M1 la raideur équivalente:

Kparallèle=k1+k3+k4

et 1/kserie= 1/kparallele +1/k2 => keq1=kserie ?

Et pour la M2 je ne vois pas trop comment calculer la raideur équivalente ? Je pourrais avoir des pistes ?

Posté par re : Structure Dynamique 14-05-17 à 18:26

Je ne suis pas sûr que tu ais compris mon message précédent... Les ressorts 3 et 4 sont bien équivalents à un ressort unique de raideur (k3+k4)=2k3.
Le ressort 1 ne doit pas être considéré en parallèle avec les ressorts 3 et 4 : il n'a pas le même raccourcissement que les ressorts 3 et 4.
Les deux solides doivent-ils osciller verticalement en restant constamment horizontaux ? Si oui :
1° : le ressort 2 doit être à la verticale du centre de gravité (le centre tout simplement ?) du solide 1.
2° : la force exercée par le ressort 1 sur le solide 2 doit constamment être égale à la force exercée par le ressort 2 sur le solide 2.
3° : le raccourcissement l1 doit à chaque instant vérifier l'égalité :
l1=l2+l3.
On peut montrer assez simplement que cela n'est possible que si k1 vérifie une relation dépendant de k2, de k3, de M1 et de M2...
Si cette relation n'est pas vérifiée, ce qui est très possible, le solide de masse M2 ne pourra pas osciller en restant horizontal et l'étude sera beaucoup plus compliquée...
Bref : l'étude est plus compliquée que ce que tu as d'abord supposé...

Posté par re : Structure Dynamique 14-05-17 à 18:50

Je suis désolée je suis un peu perdu . Je ne vois pas du tout comment vous pouvez trouver une relation avec k1 et les masses vous appliquez un PFD ?

Je pensais il y a avait juste un dépacement horizontal des 2 masses sans déformations des 2 solides.

Posté par re : Structure Dynamique 14-05-17 à 19:49

Je traite d'abord le problème en statique :
* équilibre du solide 2 : son poids est compensé par les actions des ressorts 1 et 2 qui sont de même intensité pour que le solide reste horizontal :

$k_{1}.\triangle l_{1}=k_{2}.\triangle l_{2}=\frac{1}{2}M_{2}.g\qquad\left(1\right)$

* équilibre du solide 1 sous l'action de son poids, de l'action du ressort 2 et de l'action du ressort équivalent à l'association des ressorts 3 et 4 :

$2k_{3}.\triangle l_{3}=M_{1}.g+k_{2}.\triangle l_{2}\qquad\left(2\right)$

* les solides restent horizontaux lorsque les ressorts se raccourcissent :

$\triangle l_{1}=\triangle l_{2}+\triangle l_{3}\qquad\left(3\right)$

En tenant compte de (1), la relation (2) peut aussi s'écrire :

$2k_{3}.\triangle l_{3}=\left(M_{1}+\frac{1}{2}M_{2}\right).g\qquad\left(4\right)$

En tenant compte de (4), la relation (3) devient :

$\frac{M_{2}g}{2k_{1}}=\frac{M_{2}.g}{2k_{2}}+\frac{\left(M_{1}+\frac{1}{2}M_{2}\right).g}{2k_{3}}$

Soit après simplification :

$\frac{1}{k_{1}}=\frac{1}{k_{2}}+\left(\frac{1}{2}+\frac{M_{1}}{M_{2}}\right)\cdot\frac{1}{k_{3}}$

Tu dis avoir calculé les raideurs des ressorts... Il n'est pas du tout certain que la relation précédente soit vérifiée. Si elle ne l'est pas, le solide 2 n'a aucune chance d'osciller verticalement en restant constamment horizontal...

J'ai évidemment supposé que les longueurs à vide des ressorts vérifient :

$l_{01}=l_{02}+l_{03}+e$
où e est l'épaisseur du solide 1. J'ai toujours supposés identiques les ressorts 3 et 4. J'insiste : le ressort 2 doit être positionné à la verticale du centre d'inertie du solide 1.