Inscription / Connexion Nouveau Sujet
Statiques des fluides
Bonjour , j'essaie de resoudre un exercice mais il y a quelques points que je ne comprends pas . Voici l'ennoncé de l'exercice :
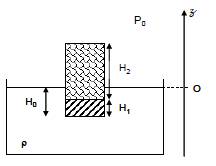
"Un solide hétérogène flotte verticalement sur un liquide de masse volumique ρ. Le solide est de forme parallélépipédique rectangle de section S et de hauteur (H1 + H2). La partie inférieure du solide, de hauteur H1 a une masse volumique ρ1 et la partie supérieure, de hauteur H2, a une masse volumique ρ2 avec ρ2 < ρ < ρ1. On suppose que la pression atmosphérique P0 est constante audessus de la surface du liquide."
1) Déterminer l'expression de la masse M du solide.M =  1V1 +
1V1 +  2V2
2V2
M = S (  1H1 +
1H1 +  2H2)
2H2)
Pourquoi M = S ( H) ?
H) ?
2) Soit H0 la hauteur de la partie immergée du solide. Déterminer l'expression de la résultante des forces de pression s'exerçant sur le solide. Quel est son sens ? Retrouver l'expression du théorème d'Archimède.
 Forces latérales = O par symetrie
Forces latérales = O par symetrie
Fsuperieur = - PoS
Finférieur = Po +  HgS
HgS
Ici , je suis d'accord que F = P*S mais pourquoi "Finférieur = Po +  HgS" ?
HgS" ?
3) Faire le bilan des forces auxquelles le solide flottant est soumis lorsqu'il est à l'équilibre, et en déduire la relation entre ρ1, H1, ρ2, H2, ρ et H0.
A l'equilibre : PA = P = Mg
Pourquoii " a l'equilibre PA = P " ?
Si quelqu'un peut m'aiguiller , je le remercie d'avance .
Bonjour Juuulie-ee,
ta premiere question est facile a expliquer : puisque le solide est un parallelepipede, de section S et de hauteur H, alors son volume est V = SH, et sa masse est bien m =  V =
V =  SH.
SH.
Le reste n'est pas tres dur non plus. Je regarde ca cet apres-midi, a moins que d'ici la un correcteur ne se propose.
A tout a l'heure,
prbebo.
2)
Somme (Forces latérales) = 0 par symétrie :
Pour les forces sur les faces horizontales :
La pression au niveau de la face supérieure du solide est la pression atmosphérique (notée Po)
On a donc Pression sur face supérieure = Po
La Force de pression sur la face supérieure du solide est verticale vers le bas, on a donc Fs = - Po.S (le "-" indique le "vers le bas")
La pression au niveau de la face inférieure du solide est la pression atmosphérique plus la pression hydrostatique (due à la hauteur Ho de la colonne d'eau)
On a donc Pression sur face inférieure = Po + Rho(eau) * g * Ho
La Force de pression sur la face inférieure du solide est verticale vers le haut, on a donc Fi = (Po + Rho(eau) * g * Ho).S
La résultante des forces de pression est : F = Fi + Fs (verticale vers le haut)
F = (Po + Rho(eau) * g * Ho).S - Po.S
F = Rho(eau) * g * Ho. S (verticale vers le haut)
Or, Ho.S est le volume immergé du solide.
Et donc |(Rho(eau) * g * Ho. S| est équivalent au poids d'un volume d'eau équivalent au volume immergé du solide.
Donc la résultante des forces de pression sur le solide est verticale vers le haut et sa norme est celle du poids du volume d'eau déplacé par le solide.
... C'est donc la poussée d'Archimède.
-----
3)
Le solide est en équilibre (ici, il est immobile) dans un référentiel terrestre qui peut être considéré comme galiléen pour le problème. Et donc la résultante des forces appliquées au solide est nulle.
... Et donc la poussée d'Archimède de l'eau sur le solide compense exactement le poids du solide.
...
-----
Sauf distraction. 


