Inscription / Connexion Nouveau Sujet
Statique du fluide
Bonjour, svp j'ai besoin d'aide.
Considerons un barrage poids à profil triangulaire fait en béton de masse volumique de base AB=L et de hauteur a. L'eau qu'il retient a une masse volumique
. L'arrêt de renversement du barrage se trouve en B.
1) Pour chaque cas où l'un des parements amont ou aval est vertical, calculer en fonction de L, et
:
Le moment par unité de largeur des forces de pression horizontale et verticale exercées sur le barrage; le moment par unité de largeur de la force de pesanteur sur le barrage et la réaction du sol sur le barrage.
2) Dans le cas où aucun parement n'est vertical, existe un tracé optimal pour la stabilité du barrage ?
Je n'ai pas fait cours sur les barrages et j'ai cherché à me documenter sur internet, mais tous les cours que je rencontre sont purement centrés sur le génie civil. Je ne sais pas ce qu'est l'arrêt de renversement ; l'axe de renversement.
Mes résultats :
1) Dans le cas où le parement amont est vertical, les forces de pression sont horizontales. Le moment élémentaire par unité de largeur par rapport à A donne et après intégration entre 0 et a, je trouve
. Les forces de pression verticales sont nulles donc le moment de ces forces est nul. Les forces de pesanteur dont l'exercice parle, je pense qu'il s'agit du poids du barrage. Sous cette considération, le moment élémentaire par unité de largeur des forces de pesanteur donne
. Après intégration,
. Pour déterminer la réaction, j'ai appliqué la condition d'équilibre. Directement, on a
où M la masse totale par unité de largeur du barrage se détermine par intégration sur le domaine et F la résultante des forces de pression.
Cas où le parement aval est vertical.
Le contact barrage-eau étant toujours plan, les forces de pression ont même direction en tout point de la surface du barrage. Le moment des forces verticales est nulle car ces forces sont toutes colinéaires à. Pour les forces horizontales, je trouve la même expression que pour le cas précédent (je ne m'attendais pas à ça) . Pour les forces volumiques, je n'ai qu'à intégrer comme tout à l'heure. Pour déterminer la réaction, il faut qu'il y ait des forces de frottement pour que le barrages soit en équilibre. On a directement
où F1 et F2sont respectivement la résultante des forces de pression horizontales et verticales.
Concernant la 3 e question, je n'ai aucune idée.
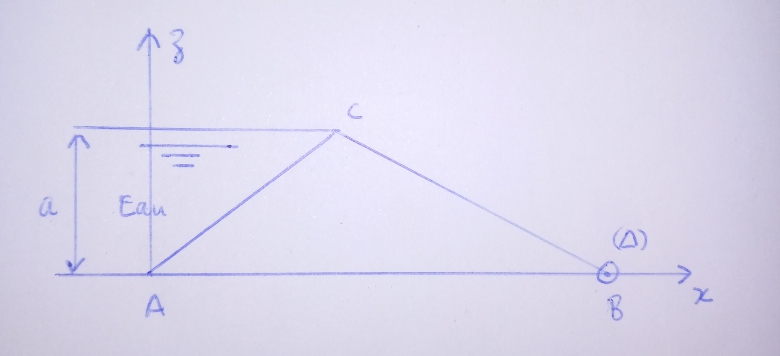
Voici le schéma.
Pour calculer tous ces moments j'ai pris l'origine en A. Doit-on le prendre au niveau de B?
Bonjour
Il faut éviter que le barrage, assimilé à un prisme, ne pivote autour de l'axe (B,y). Pour cela, on calcule le moment par rapport à l'axe (B,y) des différentes forces appliquées au barrage et on vérifie que ce moment est négatif (axe (By) orienté vers l'arrière du plan de figure pour avoir une base directe).
D'accord. Je peux alors déduire le moment en B par rapport à celui que j'ai calculer plus haut. La méthode me semble être assez longue, n'y a t-il pas une autre façon de raisonner ? Stp j'ai aussi besoin d'indications sur la dernière question.
La relation de transport du moment de A à B n'est pas nécessairement plus simple que le calcul direct du moment par rapport à l'axe (B,y). Tu peux fournir un schéma éventuellement ?
Concernant le profil optimal du barrage, je ne vois pas... Tu as fourni l'énoncé intégral ? Dans la réalité il y a tellement d'autres facteurs à prendre en compte pour l'étude de la stabilité...
C'est quel schéma éventuel que tu demandes, je ne comprends pas.
J'ai fourni l'exercice dans son intégralité. Pour les facteurs dont tu parles, je pense que si l'exercice ne les a pas mentionnés peut-être qu'on peut s'en passer.
Dans le cas où le parement est vertical, le passage du moment par rapport à (A,y) au moment par rapport à (B,y) est évident : fais un schéma si nécessaire pour t'en convaincre. Reste le moment du poids : pas trop difficile non plus.
je pense que si l'exercice ne les a pas mentionnés peut-être qu'on peut s'en passer.
effectivement, logiquement, les connaissances utiles pour résoudre la dernière question sont connues à ce niveau d'étude. C'est l'expression "tracé optimal pour la stabilité" qui ne me semble pas claire.
C'est l'expression "tracé optimal pour la stabilité" qui ne me semble pas claire.
Je pense que dans cette question, on cherche la position du point C(x,0,a) telle que le barrage offre le plus de résistance à l'eau sachant que les parements amont et aval sont obliques et A et B fixes.
Dans ce cas, il faudrait que le moment de résistance au basculement autour de l'axe (B,y) soit le plus important possible en valeur absolue ce qui suppose un moment algébrique négatif et de plus grande valeur absolue possible :
et de plus grande valeur absolue possible ???
: moment par rapport à (B,y) des forces pressantes exercées par l'eau (valeur positive ici) ;
: moment par rapport à (B,y) du poids du barrage (valeur négative ici).
Sous toutes réserves...


