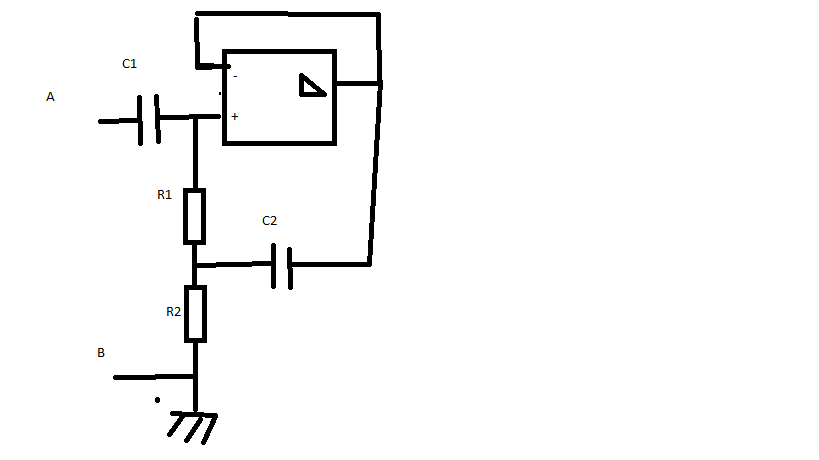
Une fois qu'on s'est rendu compte que l'unique rôle de l'ampli op est d'imposer sur la borne de droite de C2 une tension égale à celle qui existe sur la borne commune de C1 et R1, on constate que le calcul du circuit n'est pas plus difficile que celui d'un circuit passif, sans ampli op.

J'ajoute que l'ampli op assure cette fonction sans prélever aucun courant sur la borne C1-R1.

bonjour Priam !
D'abord merci de t'occuper de moi =)

Ensuite, j'ai essayé plusieurs choses et je tombe sur un résultat pour le moins étrange, donc j'ai certainement fait faux quelque part...

je note i l'intensité qui entre dans le circuit en A, i1 l'intensité qui va de D (noeud en C2, R1, R2) vers le condensateur C2 et i - i1 l'intensité qui passe dans R2 et qui ressort en B

on note V les potentiels

Comme VB = 0, pour trouver l'impédance du dipole AB, je cherche a exprimer VA / i

j'ai alors ces relations (peut etre fausse, dites le moi..)

VA - V+ (potentiel a la borne + de l'AO) = i * 1/jC1w  (1)

VD - V(-) = VD - V+ = i1 / jC2w  (*)

V+ - VD = R1 i  (**)

VD = R2 (i -i1)

(*) + (**) donne R1 i + i1/ jC2w = 0

i1 = -j R1 C2 w i

V+ = VD * R1 i
V+ = R2 i + j R1 R2 C2 w i + R1 i

on reporte tout ca dans (1) et ca nous fait finalement VA / i = (1/jC1w) + R1 + R2 + j R1 R2 C2 w

Donc Zeq = R1 + R2 + j (R1 R2 C2 w - 1/C1w )

Je ne sais pas trop trop quoi en faire. J'ai vérifié et sauf erreur, c'est bien homogene a une impédance.
Techniquement on devrait trouver que c'est équivalent à une bobine, mais je sais pas trop comment faire.

Je dois egalement trouver le facteur de qualité de ce dipole.

Est-ce que jusqu'ici ma démarche a été la bonne et est correcte ?
Comment faire pour continuer ?
Merci d'avance  

J'ai trouvé : Zeq = R1+R2 + j.(w²R1R2C1C2 - 1)/(wC1)

Ce qui est équivalent à ta réponse.

Ce n'est évidemment pas l'équivalent d'une bobine. Ce qui est d'ailleurs évident, me semble-t-il, sans aucun calcul.
Par exemple en DC, il est évident que, par la présence de C1, le courant d'entrée du circuit = 0 et que donc Z est infini... Alors que pour une bobine, on aurait un quasi court-circuit (une faible résistance)

Ce montage a une impédance très élevée en BF et en HF, et une impédance purement résistive (R1 + R2) à la pulsation w telle que w²R1R2C1C2 - 1 = 0

Il se comporte donc plutôt comme un RLC série.
-----
Sauf distraction.  

effectivement en me relisant il semblerait plutot que ca ressemble a un RLC série (sinon pourquoi me demanderait on le facteur de qualité?)

si je ne m'abuse, la forme de l'impédance d'un RLC série est de la forme : R + j(wL - 1/wC)

Donc si j'identifie ici, on a R = R1 + R2
L = R1 R2 C2
C = C1

jusque la c'est homogene

Donc Q = 1/R * sqrt (L/C)

donc Q = 1/(R1 + R2 ) * sqrt (R1 R2 C2 / C1)

Est-ce correct ?

Cela me semble juste.
-----

Reste à voir pourquoi c'était supposé simuler une bobine.

En gros, si j'ai bien compris, C1 joue le role du condensateur dans le circuit RLC classique, et le reste du montage avec l'AO simule la bobine..

Par contre l'intéret du montage....

Peut etre qu'on peut avoir plus facilement une grande inductance grace aux resistances ?