Hello

Je crois que la 2ème étape est effectivement erronée, car elle revient à dire que:

ce qui est faux (pour t'en convaincre, essaie avec a = b = 0)

Tu remarqueras également que dans la 1ère expression de F, tu peux permuter les entrées sans changer la valeur en sortie. Ce qui n'est pas le cas dans la 2nde expression

La simplification correcte me semble être:

Merci
Est ce que le tableau de Karnaugh donne toujours l'expression la plus simplifiée ?

La table de Karnaugh est en effet un outil pratique de simplification d'un système combinatoire.

Pour le système de ton exercice, cependant, la simplification est assez rapide sans mettre en oeuvre cet outil:

Est ce que le tableau suffit dans un examen pour faire la simplification ?
Et Est ce que le tableau de Karnaugh donne toujours l'expression la plus simplifiée ?

Karnaugh



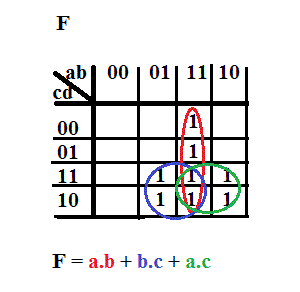
Visuel, simple, efficace, concis...

Tant que le nombre de variables n'est pas supérieur à 4 (pour les débutants)
Et jusque 5 variables avec un poil d'habitude.

Je sais j'ai fait tout ça avant et j'ai trouvé la même réponse que vous.
Mes questions sont : Est ce que le tableau suffit dans un examen pour faire la simplification ?
Et Est ce que le tableau de Karnaugh donne toujours l'expression la plus simplifiée ?

Je compatis à ta peine (je viens de lire ton autre post sur le même thème)

Tu disposes de 2 techniques pour simplifier tes expressions logiques:

1) tu utilises les règles de l'algèbre de Boole (c'est ce que j'ai fait et ce que J-P a fait dans l'autre post)

2) tu utilises un tableau de Karnaugh


La seconde technique, si tu appliques les règles d'utilisation correctement, te garantit de trouver l'expression la plus simplifiée

Par contre, elle est plus longue à mettre en oeuvre, surtout quand les propriétés des opérateurs booléens te mènent rapidement à une expression qui est "visiblement" la plus simple possible.

Et je complète, oui le tableau de Karnaugh est une méthode licite lors d'un examen (sauf indication contraire de l'énoncé bien sûr!)

Comme je l'ai écrit ...

Si le nombre de variables ne dépasse pas 4 (5 pour les "pros"), il est TOUJOURS possible de simplifier l'équation à l'aide d'un tableau de Karnaugh, comme c'est toujours possible aussi par d'autres méthodes (Mc Cluskey par exemple).

Néanmoins ...
Le résultat obtenu pour la "qualité" de la simplification dépend de l'habilité à se servir des outils (que ce soit Karnaugh, ou Mc Cluskey ou autres).

Dans le cas présent, la simplification "optimale" est tellement "évidente" par Karnaugh qu'il est quasi impossible (même pour les maladroits) de ne pas la trouver ...

Pour certains cas plus "tordus", cela dépendra de "l'habilité" de l'utilisateur.

D'ailleurs, on ne peut pas définir (dans maints cas) ce qu'on entend par "simplification optimale".

Merci beaucoup pour vos réponses sur les deux posts mais le prof fait des erreurs et ne revient pas alors sur la bonne réponse ou maintient ce que je pense être faux en ne s'expliquant pas clairement.
Donc je me mets à plus travailler ces cours et exercices...
j'ai du mal a distinguer ce qu'est la bonne méthode surtout que ces réponse a nos questions sont vagues et changeantes...

Merci encore

Je risque donc de vous demander des conseils à vous et à mon frère dans le supérieur....