Inscription / Connexion Nouveau Sujet
Sens courant
Bonsoir,
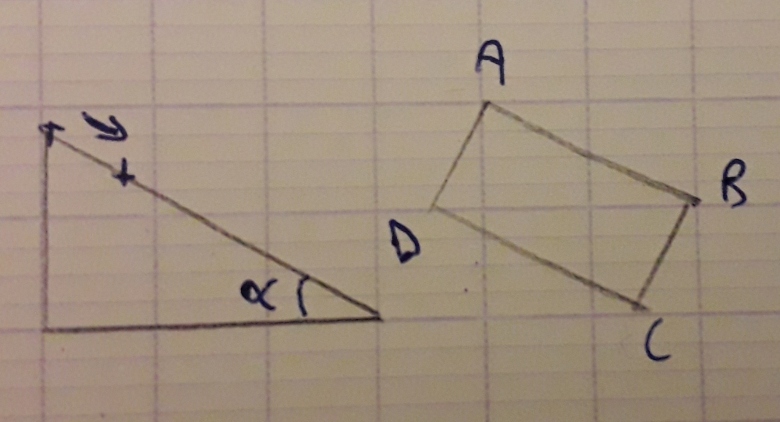
Je cherche le sens du courant dans le circuit ABCD. BC est une tige conductrice qui glisse sans frottement le long du plan incliné d'angle  . AB et DC sont des rails métalliques. AB est relié par un fil ayant une résistance électrique, les résistances électriques des rails et de la tige sont quant a elles négligeable. Il règne un champ magnétique uniforme, vertical, dirigé vers le haut.
. AB et DC sont des rails métalliques. AB est relié par un fil ayant une résistance électrique, les résistances électriques des rails et de la tige sont quant a elles négligeable. Il règne un champ magnétique uniforme, vertical, dirigé vers le haut.
Je ne vois pas trop comment faire, je connait la règle de la main droite pour connaitre le sens de chaque vecteur mais je ne sais pas comment est dirigé la force de Laplace. Je sais également que le sens conventionnel du courant électrique va du + au - .
Ton schéma n'est pas complet. Le glissement de la tige sur les rails modifie la surface du circuit et donc entraîne une variation de flux magnétique en fonction du temps. Apparaît alors un courant induit...
Essaie de faire un schéma soigné en lui donnant une orientation.
Quelles sont les questions posées ? Un énoncé complet accompagné d'un scan du schéma qui l'accompagne serait bien utile.
BC glisse et a une vitesse initiale. À cet instant, BC rentre dans la zone contenant le champ magnétique. Il faut connaitre le sens du courant à cet instant précis.
Le premier schéma est un schéma de coupe, le premier point montre AD et le deuxième BC, le deuxième schéma est une vision par-dessus.
Oui, même si je n'ai pas tout compris.
Le système s'oppose à la cause de l'induction (la vitesse).
Donc la force de Laplace à la même direction que la vitesse mais de sens opposé. Ainsi la force de Laplace a pour sens de A à D. Alors, le courant électrique va de A à B et de C à D.
Disons que la force de Laplace va avoir une composante qui s'oppose au glissement vers le bas de la tige BC. La force de Laplace est nécessairement perpendiculaire au vecteur B, elle ne peut donc pas être colinéaire aux rails.
Essaie de compléter ton schéma en y indiquant les différents vecteurs utiles : vecteur champ magnétique B, vecteur vitesse de glissement de la tige, vecteur force de Laplace.
Remarque : je ne sais pas si toutes les notations sont imposées par l'énoncé. C'est une très mauvaise idée de donner deux significations différentes à la lettre B...
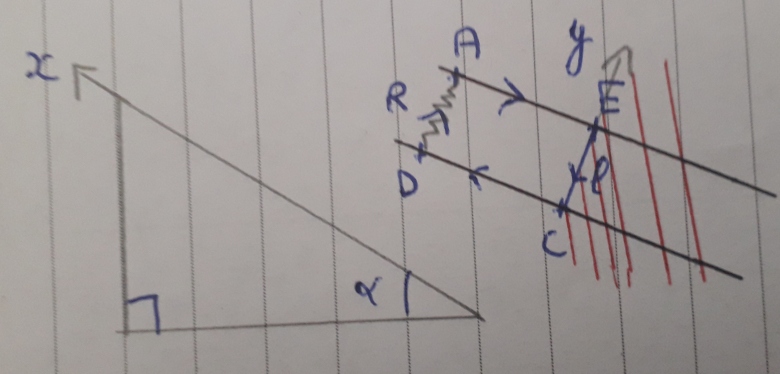
Remplacons B par E et la zone hachurée rouge représente le champ magnétique.
Le courant serait de C vers E.

D'accord, à cet instant, le courant fait le "tour" du rectangle ou on peut juste dire que E est (+) et C est (-) ?
La tige EC glisse sur les deux rails inclinés et parallèles. Si je comprends bien l'énoncé, le circuit est fermé par un fil conducteur de résistance R qui relie les deux extrémités supérieures (A et D semble-t-il) des rails. Le courant induit circule donc dans ce circuit (ECDA) dans le sens E C
C D
D A.
A.
Merci.
Voici le schéma de la situation. La figure 1 représente l'expérimentation vu de côté tandis que la figure 2 la représente vu de dessus. La zone hachurée rouge représente une région de l'espace où règne un champ magnétique uniforme, vertical, ascendant, d'intensité B.
Je cherche à determiner I0 qui apparaît dans le circuit AECD et qui correspond à l'instant t=0 où la tige métallique pénétre le champ magnétique avec une vitesse v0.
Le prof nous a donné la réponse: I0=Blv0cos( )/R et nous a dit qu'il faut utiliser le flux.
)/R et nous a dit qu'il faut utiliser le flux.
Voici ce que j'ai fait: Appelons le flux de champ magnétique M:  M=
M= B.dS=
B.dS= B*dS=B*l*dx
B*dS=B*l*dx
Je remarque que dx/dt=v et que le projetté de B sur l'ax donne B*cos( ) mais je n'arrive pas à faire la question.
) mais je n'arrive pas à faire la question.
La variation élémentaire de flux (ou le flux coupé élémentaire, je ne sais pas comment tu raisonnes habituellement) fait intervenir le produit scalaire
où le vecteur
caractérise la surface en étant perpendiculaire à celle-ci. La formule du produit scalaire conduit donc à :
Je pense que tu as compris la suite. Pose d'autres questions si tu le juges utile.
Ah oui c'est vrai que ces vecteurs ne sont pas colinéaires.
Je ne vois pas comment passer du flux au courant.
Je n'ai pas fait attention à l'orientation du vecteur surface en fonction de l'orientation du circuit. Compte tenu de l'orientation choisi, le vecteur est perpendiculaire au circuit comme déjà écrit mais orienté vers le bas. Tu as donc :
. Pendant la durée dt, la tige parcourt la distance v.dt ; elle balaie donc une surface dS=v.l.dt .
D'où la fém induite :
Loi de Pouillet :
A adapter aux conditions initiales...
Si tu as quelques soucis avec l'orientation du vecteur surface, tu peux consulter le post suivant à partir du message du 22.03.20 à 12h43 :
![]() auto induction
auto induction
Dernière question, lorsque l'on fait le produit scalaire c'est par rapport à la surface ou le vecteur n dirigé vers l'extérieur ? Le produit scalaire donne cos(90+ )=-sin
)=-sin ) ou cos(
) ou cos( ) ?
) ?
Ah non ca fait cos(180- )=-cos(
)=-cos( ) donc dflux=Blcos
) donc dflux=Blcos dx
dx
e=-dflux/dt et comme la vitesse est orienté de l'autre coté ca donne bien e=Blcosv


