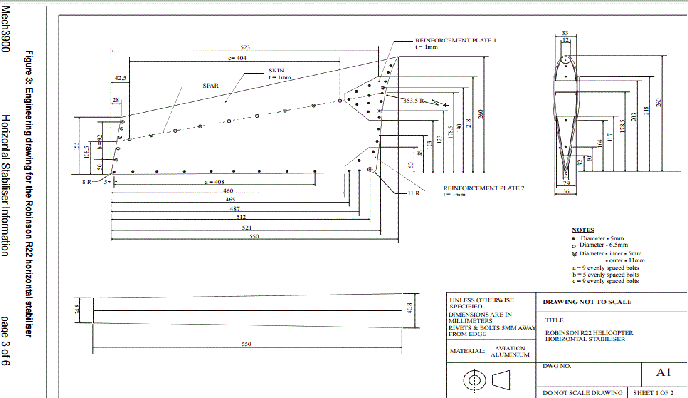
Donc en fait mon problème est que je ne vois pas comment calculer le cross sectional area, et par consequent je bloque aussi sur le moment quadratique.

Si quelqu'un pouvait me donner un piste. Merci

Hello

Je dirais que pour calculer la section plane du déflecteur, tu dois utiliser le fichier excel qui, si je comprends bien, t'a permis de tracer la 1ere figure. Je ne connais pas son contenu, mais il doit te donner pour une certaine côte z, y(x). Pour 2 valeurs successives de x la surface élémentaire sera "approximée" par



N'hésite pas à partager plus complètement les infos dont tu disposes, parce que là ...

D'accord, merci pour ton aide dirace.

Donc voila le ficheir excel, donc en fait on dispose de Y en fonction de X, mais cest deux valeur dependent ensuite d'une troisieme valeur qui est c.

Ensuite pour trouver la deflection et le stress, on dispose d'un autre fichier excel avec les pressions.

Mais en fait deja mon premeir soucis c'est avec ces valeur dans le excel, je ne sais pas comment les analyser (c'est moi qui ai fait le graph, donc il est peut etre faux).

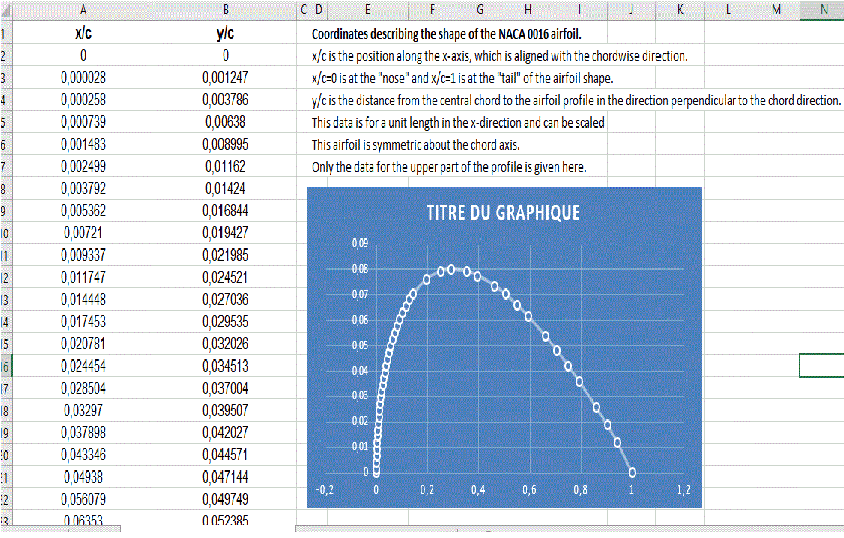
L'énoncé te dit je crois de faire la moyenne entre les valeurs des cordes à l'implanture et au saumon.

Donc  

-le divisé était une coquille dans transcription en Latex dans mon précédent msg
-hypothèse faite que le profil est symétrique par rapport à l'axe comme ton premier schéma  semble l'indiquer

Ok, d'accord, merci beaucoup, du coup maintenant que j'ai la section, je suis censé trouver le barycentre(Xa;Ya) , donc deja comme on fait l'hypothèse d'un solide homogène, et symétrique sur 0x, on peut déjà affirmer que Yb=0.

Maintenant le problème, c'est que d'habitude pour trouver un barycentre  on utilise l'intégration de la fonction, la avec des points je ne sais pas comment faire.

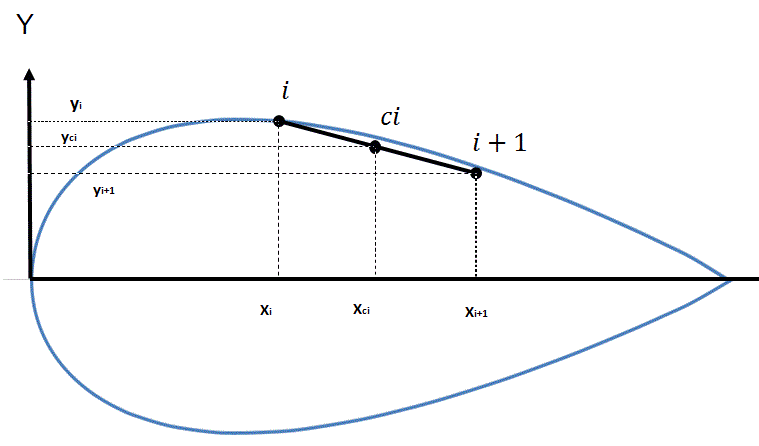
L'expression intégrale que tu utilises d'habitude doit être quelque chose comme (en utilisant "au mieux" les notations utilisées jusqu'alors):



Que tu "approximes" ici avec les données de ton tableur avec une somme discrète pour les valeurs successives de (de 0 à c) où   devient

On dispose aussi de ça que je viens de trouver :



Mais on ne sait pas a quoi correspond Ai

Ensuite on a:




enfin:


Donc mon problème, c'est que je ne comprend pas ces formules

J'ai un train à prendre ... mais si pas d'aide dans l'intervalle je regarderai en fin d'aprèm ...
Tu vas y arriver

D'accord merci beaucoup, je vois la prof entre temps, je lui demanderais, je te dis ce soir si j'ai  bien compris. Mais en tout cas merci beaucoup pour ton aide!!

Il y a le wifi dans le train

est la surface élémentaire entre et

Ensuite te sont données les coordonnées du barycentre, ce qui te posait pbm tout à l'heure: on est passé d'une sommation continue, à une approximation par une sommation dicrète sur les surfaces successives (cf. notre échange de 12:12)

Enfin c'est l'application du Théorème de Huyguens

Ca va mieux?

Ok dak, donc j'ai pense avoire compris, le probleme c'est que je trouve un Xcp de 0,022406093.
Ce qui a premiere vu est faux. j'ai revu mes calcul excel 10 fois je vois pas le problème...

Ensuite pour trouver le moment quadratique si j'ai utiliser les formule du dessus du coup j'ai calculer deux I, un pour le tip, l'autre root, ensuite on j'ai pris la moyenne. Je vois pas ou utiliser Huygens?

Puis-je t'envoyer mon excel par mail, si tu a le temps de jeter un coup d'oeil?

bien sûr, email bien reçu. Je regarde.