Bonsoir
Sans indication du contexte de ton étude, difficile de répondre de façon rigoureuse. Une réponse possible  en supposant l'atmosphère homogène.
En théorie cinétique des gaz, on démontre que la vitesse quadratique moyenne v* des molécules de gaz est proportionnelle à , la constante de proportionnalité dépendant de l'atomicité du gaz (nombre d'atome(s) par molécule) :



D'autre part, la vitesse de libération, c'est à dire la vitesse minimale que doit avoir une molécule pour s'échapper définitivement de la planète malgré l'attraction gravitationnelle est : .
La thermo statistique, confirmée par l'expérience, montre qu'un équilibre s'établit pour


avec M_p : masse de la planète et G : constante universelle de gravitation.
Cela explique pourquoi, sur terre, il n'y a plus de dihydrogène ; ces molécules sont suffisamment légères pour que leur vitesse quadratique moyenne soit très supérieure à leur vitesse de libération.
Petit problème par rapport à ton énoncé :
On obtient   proportionnel à et pas simplement inversement proportionnel à r_p.
On peut faire intervenir g_o : intensité de la pesanteur au niveau du sol :


Problème : on obtient ainsi proportionnel et non inversement proportionnel à r_p.
Tout cela sans garantie : ton énoncé me parait bien imprécis et quelque chose m'a peut-être échappé. Sans plus d'explications, cela me parait difficile à ce niveau...

Cela est peut être naïf, mais il me semble que puisque une des hypothèses de l'énoncé est que la planète est sphérique et homogène sa masse est proportionnelle à (r_p)³ donc   est proportionnel à r_p et H=RT/Mg est inversement propotionnel à r_p (car je suppose que le "g" de la relation H=RT/Mg est l'accélération de la pesanteur au niveau du sol g₀)
Qu'en pensez vous ?

Cela n'a rien de naïf odbug1.

C'est aussi la réponse que j'aurai faite... en espérant que le "H=RT/Mg " de l'énoncé soit plutôt "H=RT/(Mg) , ce qui n'est pas du tout la même chose.

L'analyse dimensionnelle confirme :

Ok merci beaucoup, je vais essayer. J'avais aussi oublié une hypothèse peut être importante: l'atmosphère est supposé être un gaz parfait.
Mais je ne sais pas si c'est utile ici (peut être toucher à T?), je pense que ca l'est pour les questions ultérieures.

Tout est dans le message de odbugt1 ... pour la partie de l'énoncé mise sur le site.

Je reprends ce qu'il a écrit en détaillant (bien que c'était, je pense, limpide) :
-----
Il s'agit bien de go dans la formule H = RT/(M.go)

Voir par exemple sur le lien :  
Au chapitre : "Isothermal-barotropic approximation and scale height"

Dans les conditions de l'énoncé de l'exercice présent, RT/M est une constante, donc H est inversement proportionnel à go.

Or go = G.Mp/rp² avec  G la constante de gravitation, Mp la masse de la planete de rayon rp et supposée sphérique et homogène, on a donc :

Mp = 4/3.Pi.rp³ * Rho(planete) (avec Rho(planete) = constante).

--> Mp est proportionnel à r³ (Mp = k.rp³ avec k une constante)

go = G.k.rp³/rp² = G.k.rp

-->  go est proportionnel à rp (puisque G.k = constante)

Et comme H est inversement proportionnel à go, H est proportionnel à 1/rp

... évidemment dans les conditions de l'énoncé, soit  pour une planète homogène sphérique et de masse volumique donnée.

Sauf distraction.  

Bonjour
Je suis effectivement sûrement aller chercher trop loin pour un problème de Sup même si la théorie très simplifiée que j'expose à de nombreuses applications : elle permet d'expliquer pourquoi certains astres (la lune par exemple) n'ont pas d'atmosphère gazeuse, pourquoi d'autres astres  (la terre) n'ont pas dans leur atmosphère de gaz légers (H₂...)
Pour en revenir à ce que pourrait être la réponse souhaitée : il me semble qu'il s'agit de comparer les valeurs de H pour diverses planètes. Dans ces conditions, considérer la planète comme une boule homogène de masse volumique _p conduit à g_o proportionnel à _p.r_p ... Pourquoi privilégier le rôle de r_p ?
On retrouve la valeur de H dans l'expression de la variation de la pression atmosphérique pour une atmosphère isotherme avec l'altitude z(<<r_p) :

Il y a autre chose qui me gêne, en rapport avec le message de larapa du 05-08-17 à 10:39.
Outre l'objection de mon message précédent, passer de g_o proportionnel à
_p.r_p à H inversement proportionnel à _p.r_p  nécessite T/M invariant d'une planète à l'autre, ce qui bien sûr est faux !
Donc finalement, mon premier message... De toutes façons, sans connaître l'énoncé complet qui permettrait d'avoir des informations sur le but final de l'exercice...

L'énoncé (jusque là) ne parle pas de planètes différentes.

L'énoncé dit : "Il faut montrer que si la planete est sphérique et homogène, H est proportionnel à 1/rp"

Avec "la" article défini singulier.

Bien évidemment, l'énoncé n'est pas clair puisqu'il n'y en a vraisemblablement qu'un extrait (forcément retiré de son contexte)
... et par là toute supposition permet de répondre à peu près n'importe quoi.

Bonsoir
Impossible effectivement de savoir exactement ce qu'attend exactement le concepteur de l'énoncé. Il est cependant possible de réfléchir, par simple curiosité scientifique,  à ce qu'implique physiquement la phrase de l'énoncé concernant "H inversement proportionnel à r_p". En assimilant l'atmosphère à un gaz parfait en équilibre à température uniforme, la variation de pression avec l'altitude z est donnée par la relation que j'ai rappelée dans mon message précédent :

On peut raisonnablement considérer l'exponentielle comme nulle pour z>5H ; ce qui revient à dire que la hauteur de gaz entourant la planète est de l'ordre de 5H. Elle est donc, selon l'énoncé, inversement proportionnelle à r_p. Ainsi, plus le rayon de la planète serait faible, plus l'épaisseur de gaz l'entourant serait grande ; cela est évidemment absurde. Par exemple la lune de relativement faible rayon n'a pas d'atmosphère gazeuse car, comme déjà expliqué, la  valeur théorique de la vitesse quadratique moyenne des molécules de gaz est très largement supérieure à la vitesse de libération.
En revanche, en comparant comme je l'ai fait dans mon message du   04-08-17 à 22:49, vitesse quadratique moyenne et vitesse de libération, je suis arrivé à la conclusion d'une valeur de H proportionnelle à r_p. La valeur de H a pu être mesurée sur certaines planète. J'ai eu la curiosité de représenter graphiquement, les variations de H en fonction de r_p pour quelques planètes. On constate que la modélisation que j'ai présentée hier est loin d'être parfaitement vérifiée avec en particulier une exception notable pour la terre. Tout de même, ce modèle est plus proche de la réalité que celui proposé par l'énoncé !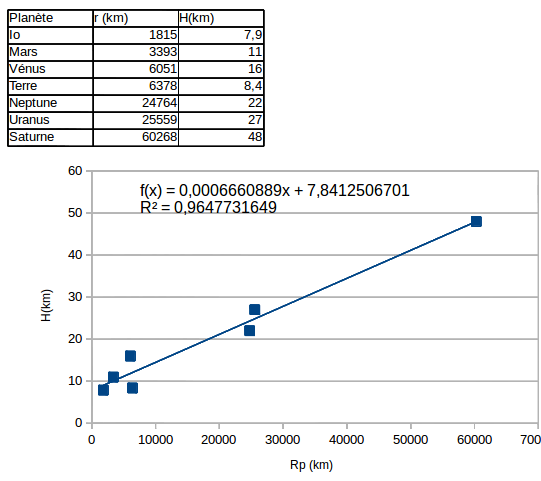



***Image recadrée***

Oui mais ... ce n'est pas ce qui est demandé ici.

Il fallait comprendre :

Montrer que pour une planète possédant une atmosphère de masse molaire M, la planète étant sphérique de rayon rp et homogène, de masse volumique Rho et à température uniforme T.
H = RT/(M.go) est proportionnelle à 1/rp

Tout le reste est intéressant ... mais hors demande de l'exercice tel qu'il est posé.
----------------
Je ne pense pas que ce qu'avance l'énoncé est absurde ... mais il fait évidemment en voir les limites et l'utiliser avec les précautions d'usage.

Si on utilise la formule H=RT/(M.go) et qu'on l'applique aux planètes de ton message (en allant chercher les valeurs de M, go et T sur wiki), on trouve :

Pour Mars : H = 10,7 km
Pour Vénus : H = 15,6 km
Pour la Terre : H = 8 km
Pour Uranus : H = 28 km
Pour Saturne : H =  31 km ??

On peut donc utiliser la relation H=RT/(M.go) pour des résultats plus que "honnètes".

A partir de là, comme go = GMp/rp² et que (avec les données de l'énoncé) Mp = 4/3.Pi.rp³ on peut mathématiquement en déduire que :

H = 3R/(4.Pi.G) * T/(M * Rho) * 1/rp  (pas vérifié)

Donc, que pour une planète avec M comme masse molaire de l'atmosphère, T  et Rho imposés, H est proportionnel à 1/rp

Et ceci n'a évidemment rien à voir avec des comparaisons pour des planètes de différents M, T ou Rho.

Il ne faut pas non plus pousser des raisonnements à la limite comme rp --> 0 (qui avec un rho donné, correspondrait à une planète de masse nulle, ce qui ne rime à rien, puisque H n'est pas alors défini)

Cela veut seulement dire, par exemple, que comme on a H = 8 km pour la Terre, si on avait une planète de même Rho que la Terre, de même composition d'atmosphère à la même température que la Terre, mais avec un rayon 2 fois plus grand (par exemple) ... on aurait pour cette planète H' = H/2 = 4 km (environ bien entendu)

Je ne suis pas d'accord, mais ce sera mon dernier post sur ce sujet.

Tu t'obstines à vouloir raisonner sur un problème différent de celui de l'énoncé.

"pour une planète donnée, M n'est pas une variable indépendante, elle dépend fortement des autres paramètres de la planète."

On s'en fout l'énoncé impose T, M et Rho(planète) (même si il n'en donne pas de valeurs numériques)

Et pour autant de ne pas chercher des misères en allant aux limites (comme rp --> 0), mon calcul (par exemple avec la Terre et une autre planète de rayon double mais de même composition d'atmosphère, de même T et de même masse volumique) est licite ... et va dans le sens de la variation de H proportionnellement à 1/rp.

Ceci ne signifie pas qu'il soit possible dans toutes circonstances d'avoir une même composition d'atmosphère (donc un même M) pour différentes planètes de taille très différentes ... mais dans le cas de l'énoncé (du moins dans la partie donnée), on est censé raisonner avec M, T et Rho donnés (comme paramètres ... donc invariants en cours d'étude)

L'énoncé na va pas, à mon avis, plus loin que cela.

Peut-être le fera-t-il plus loin.

Bonjour
Je ne vais pas intervenir à nouveau sur le fond mais juste une tentative de synthèse pour que larapa s'y retrouve :
1° : compte tenu du niveau auquel est posé ce problème et de l'absence de progressivité dans la question, il est quasi certain que la réponse attendue est celle fournie par odbugt1 dans son message de  05-08-17 à 00:01.
2° : ma première réponse "tapait" donc d'entrée un peu trop haut comme d'ailleurs je l'écrivait en fin de ce premier message.
3° : tout cela étant dit et admis, il n'est pas interdit de réfléchir et d'approfondir un peu plus, même si cela n'est pas immédiatement utile dans cet exercice. La réalité est complexe, beaucoup plus évidemment que ce que j'en ait dit dans mes différents messages. Une chose est cependant incontestable : la présence ou non de molécules d'un gaz donnée dans l'atmosphère dépend de sa masse molaire, de sa vitesse cinétique donc de T et de la vitesse de libération, donc de g_o et de r_p. La composition chimique d'une atmosphère, donc M, dépend de g_o, de r_p et de T. Ainsi affirmer que H est inversement proportionnel à r_p n'est pas vérifié en réalité  ...

"Ainsi affirmer que H est inversement proportionnel à rp n'est pas vérifié en réalité  ..."

Bien sûr que si ... à condition de respecter les conditions imposées par l'énoncé et pas en s'en écartant du tout au tout en répondant à autre chose que ce qui est demandé.