Inscription / Connexion Nouveau Sujet
Roulement sans glissement
Re!
La prochaine est vite arrivée, Coll :p
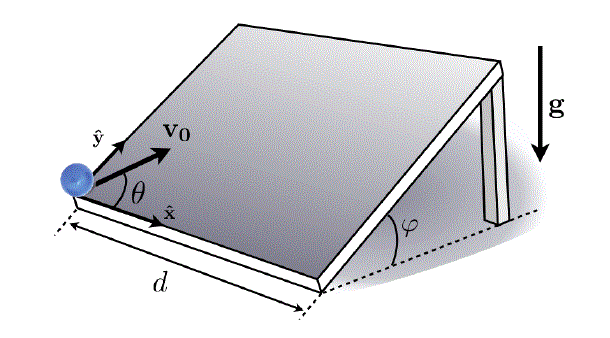
Dans cette énoncé, il nous faut calculer la distance ymax que va atteindre la bille. Le moment d'inertie de la bille est I=(2/5)MR^2. On suppose que la bille roule sans glissement.
Je suis un peu perdu avec le faite que ce la bille roule sans glisser :/ Si je devais faire un schéma des forces, comment devrais-je faire? Faut il que je représente un vecteur force de frottement au point de contact et de direction opposé à la direction ? Bref, je ne sais..
Energie cinétique au départ : Ec = (1/2).m.Vo² + (1/2) * (2/5).m.R²*(vo/R)² = 0,7.m.Vo²
Energie potentielle au départ : 0
Pour une certaine valeur de y :
Energie potentielle : m.g.y.sin(Phi)
---> énergie cinétique: Ec(y) = 0,7.m.Vo² - m.g.y.sin(Phi)
Conservation de l'énergie mécanique :
0,7.m.Vo² - m.g.y.sin(Phi) = 0,7.m.v²
v² = Vo² - g.y.sin(Phi)/0,7
---
Pas de force sur la bille dans la direction Ox ---> composante de la vitesse suivant Ox = Constante (Vo.cos(theta))
Lorsque V = Vo.cos(theta), la bille est au sommet de sa trajectoire --->
Vo².cos²(theta) = Vo² - g.y.sin(Phi)/0,7 qui correspond à y max
Vo²(1-cos²(theta)) = g.ymax.sin(Phi)/0,7
Vo².sin²(theta) = g.ymax.sin(Phi)/0,7
ymax = 0,7.Vo².sin²(theta)/(g.sin(Phi))
-----
Sauf distraction. 


