Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Rotationnel et divergence

Posté par
archange12 05-10-21 à 17:56

Bonjour (: , comme l'année dernière j'ai de nouveau besoin de votre aide!
Je bloque sur un exercice sur les rotationnels et les divergences.

---------- ENONCE-----------

1 Démontrer les relations suivantes :

\vec{rot}(\vec{grad}(U)) = \vec{0}

div(\vec{rot}(\vec{E})) = 0

\vec{rot}(a*\vec{V}) = a*\vec{rot}(\vec{V}) + \vec{grad}(a) \wedge \vec{V}

div(a*\vec{V}) = a*div(\vec{V}) + \vec{grad}(a)\bullet  \vec{V}

div(\vec{U}\wedge  \vec{V}) = \vec{V}\bullet \vec{rot}(\vec{U}) - \vec{U}\bullet \vec{rot}(\vec{V})

2 Soit  dans lequel E et k sont des vecteurs constants. Calculer div(V) et rot(V)

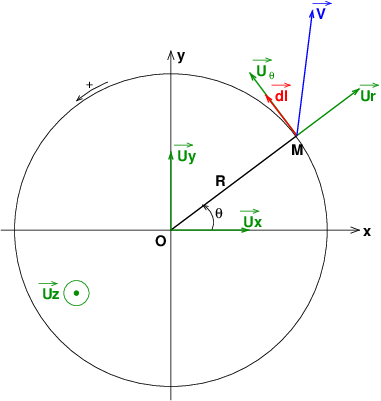
3 On considère le vecteur V de composantes Vx = xy et Vy = x2/2 +3x
. En utilisant le théorème de Stokes, calculer la circulation de V le long du cercle de centre O et de rayon R = 3 cm.

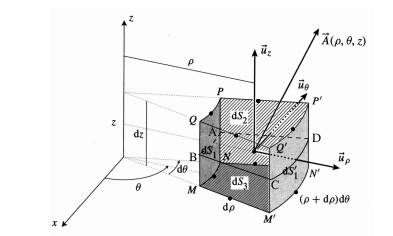
4 On considère un volume élémentaire de cylindre MNPQM'N'P'Q' centré sur le point C suivant :

On note A(ρ ,θ,z) un vecteur d'origine C.

4.1 Calculer le flux du vecteur A à travers la surface totale du volume élémentaire
(la normale étant orientée sur chaque face vers l'extérieur).

4.2 En utilisant le théorème de Green-Ostrogradsky, en déduire l'expression de la
divergence de A en coordonnées cylindriques.

4.3 Calculer la circulation du vecteur A e long des trajets orientés : M'N'P'Q',
MQQ'M' et M'N'NM.

4.4 En déduire l'expression du rotationnel de A en coordonnées cylindriques.

-------------
Je préfère laisser de coté pour l'instant la partie 4.
Pour la question 1, j'ai réussis les deux premières démonstration, pour la première j'ai déjà exprimer gradU puis rotU' , j'ai ensuite remplacé et j'ai bien trouvé le vecteur 0, j'ai fais la même méthode pour la deuxième.
Pour les trois démonstrations d'après j'ai essayé d'exprimer la partie gauche et j'ai essayé de retomber sur la partie droite, mais je n'y arrive pas, je ne vois pas comment faire.

Pour la question 2, je ne vois pas comment calculer la divergence et le rotationnel pour un vecteur en fonction d'un autre vecteur (ici r).

Pour la question 3 je ne comprend pas comment il faut faire.
-------------

J'espère que vous pourrez m'aider (:

en bref j'ai besoin d'aide pour la question 2,3 et les 3 dernières démonstrations de la question 1.

Posté par
vanoisere : Rotationnel et divergence 05-10-21 à 19:00

Bonjour
Les deux premières formules doivent effectivement être connues "par coeur" car elles servent à de très nombreuses démonstrations.
Pour les autres : ton professeurs exagère un peu : elles sont fournies sans démonstrations dans tous les problèmes de concours de l'éducation nationale (admissions dans les grandes écoles scientifiques, CAPES, Agrégation...). On peut s'en sortir assez rapidement grâce aux propriétés de l'opérateur "nabla", sinon, la démonstration en utilisant les coordonnées cartésiennes est longue et laborieuse.
Je ne comprends pas bien la question 2 ; l'énoncé est-il complet ?
Pour la question 3 : connais-tu l'énoncé du théorème de Stokes ? Il s'agit de le vérifier pour un vecteur \vec V dont les composantes dans un repère cartésien son fournies.
Le document ci-dessous pourra peut-être t'aider mais il ne fournit pas toutes les démonstration de la question 1.

Posté par
archange12re : Rotationnel et divergence 05-10-21 à 19:58

Merci pour votre réponse
D'accord pour la question 1.
ha oui excusez moi j'ai oublié l'expression :

2 : Soit \vec{V}( \vec{r}) = \vec{E}exp(i\vec{k}\bullet \vec{r})  dans lequel E et k sont des vecteurs constants. Calculer div(V) et rot(V).

3. D'accord, je vais essayer je reviens vers vous (:

Posté par
vanoisere : Rotationnel et divergence 05-10-21 à 20:06

Pour 2 : il faut utiliser les formules 3 et 4 de ta liste initiale.

Posté par
archange12re : Rotationnel et divergence 05-10-21 à 20:27

Avec a = E et V = exp(ik.r) ?

Pour la question 3 il faut alors montrer que la partie gauche du théorème de Stokes est égal à la partie droite en utilisant les données de l'énoncé ? Je ne vois pas trop comment commencer

Posté par
vanoisere : Rotationnel et divergence 05-10-21 à 23:07

Ici : \overrightarrow{V}=\overrightarrow{E} : vecteur indépendant des coordonnées (x,y,z) : la divergence et le rotationnel ont des expressions particulièrement simples ! Reste donc seulement à calculer le vecteur gradient de a=k=\exp\left(\left[i\left(k_{x}.x+k_{y}.y+k_{z}.z\right)\right]\right) où les trois composantes du vecteur \overrightarrow{k} sont des constantes.

Pour la questions 3 : tu connais les composantes Vx et Vy en fonction de x et de y du vecteur \overrightarrow{V}. Tu peux donc calculer les composantes de \overrightarrow{rot}\left(\overrightarrow{V}\right) puis calculer le flux de ce vecteur à travers le disque délimité par le cercle de centre O et de rayon R.

D'autre part , tu calcules la circulation du vecteur \vec V le long du cercle. N'oublie pas que la circulation élémentaire s'écrit :

dC=\overrightarrow{V}.\overrightarrow{dl}=V_{x}.dx+V_{y}.dy.

Attention à ce que le sens positif de circulation le long du cercle soit bien cohérent avec l'orientation du vecteur \overrightarrow{dS} dans le calcul du flux pour ne pas avoir de problème de signe. Rappelle-toi la règle du ”tire-bouchon de Maxwell”...

Tu devrais ainsi, dans ce cas particulier, vérifier le théorème de Stokes.

Posté par
archange12re : Rotationnel et divergence 06-10-21 à 21:07

Pour la question 2 pour div(V) j'obtiens :
P = exp(i[kx {\bullet} x+ky {\bullet} y+kz {\bullet} z])
div(\vec{V}) = P * (\partial Ex/\partial x + \partial Ey/\partial y +\partial Ez/\partial z) + ikx*P*Ex+iky*P*Ey+ikz*P*Ez

Est ce que je dois aller plus loin ? et si oui comment ?

Pour la question 3 cela veux dire que V n'a pas de composante pour z ?
donc Vz vaut 0 ? si c'est bien cela je trouve alors pour rot(V) :

\vec{rot}(\vec{V}) = \begin{pmatrix} 0 - 0 \\ 0 - 0 \\ (x+3) - x = 3 \end{pmatrix}

Est ce correct ?

Posté par
vanoisere : Rotationnel et divergence 06-10-21 à 21:14

D'accord avec toi pour la question 3 ; le vecteur rotationnel étant constant et perpendiculaire au plan du disque, le flux de ce vecteur est immédiat. Concernant le calcul direct de la circulation, tu peux utiliser les coordonnées polaires...
Pour la question 2 : le vecteur \vec E étant un vecteur constant, sa divergence est nulle et son rotationnel est le vecteur nul. Reste donc le calcul du gradient de a avec :
a=\exp\left(\left[i\left(k_{x}.x+k_{y}.y+k_{z}.z\right)\right]\right).

Posté par
archange12re : Rotationnel et divergence 06-10-21 à 21:31

Ha oui d'accord pour la question 2

Pour la question 3 je ne comprend pas trop comment calculer la circulation

Posté par
vanoisere : Rotationnel et divergence 06-10-21 à 23:37

Citation :
Pour la question 3 je ne comprend pas trop comment calculer la circulation

Il s'agit de la circulation le long du cercle. On s'intéresse donc maintenant uniquement aux points M tels que :
x=R.cos ; y=R.sin()
avec variant de zéro à 2 rad. On calcule les différentielles :
dx=-R.sin().d ; dy=R.cos().d
Tu reportes tout cela dans l'expression de la circulation élémentaire dC que je t'ai fournie hier soir à 23h07 et tu intègres entre zéro et 2.
C'est un peu plus "calculatoire" que le calcul du flux du rotationnel mais on obtient heureusement le même résultat.

Posté par
archange12re : Rotationnel et divergence 08-10-21 à 10:18

J'ai calculé l'intégrale et je trouve 0, est ce que cela vous semble correcte ? Je n'est pas bien compris à quoi correspond cette integrale pouvait m'expliquer s'il vous plaît ?

Posté par
vanoisere : Rotationnel et divergence 08-10-21 à 14:29

Tu as obtenu : \overrightarrow{rot}\left(\overrightarrow{V}\right)=3\overrightarrow{u_{z}} (voir figure ci-dessous pour les notations).

En choisissant comme sens de circulation positive le sens trigonométrique, la règle du ”tire-bouchon de Maxwell” conduit à orienter chaque vecteur surface élémentaire suivant \overrightarrow{u_{z}} .

Le flux du rotationnel à travers le disque de centre O et de rayon R s'écrit ainsi :

\iint_{disque}\overrightarrow{rot}\left(\overrightarrow{V}\right).\overrightarrow{dS}=\iint_{disque}3\overrightarrow{u_{z}}.dS.\overrightarrow{u_{z}}=\iint_{disque}3.dS=3S=3\pi R^{2}

Pour calculer la circulation du vecteur \overrightarrow{V} le long du cercle, il faut imaginer un point M de ce cercle de coordonnées (x,y) qui subit un déplacement élémentaire \overrightarrow{dl} le long de ce cercle.La circulation élémentaire est, par définition :

dC=\overrightarrow{V}.\overrightarrow{dl}=V_{x}.dx+V_{y}.dy.

Pour se ramener à une intégrale (presque) simple en évitant la présence de deux variables, on passe aux coordonnées polaires comme expliqué dans mon message du 06-10-21 à 23:37 ;

V_{x}=x.y=R^{2}.\cos\left(\theta\right).\sin\left(\theta\right)\quad;\quad dx=-R.\sin\left(\theta\right).d\theta \\ \\ V_{y}=\frac{x^{2}}{2}+3x=\frac{R^{2}}{2}\cos^{2}\left(\theta\right)+3R.\cos\left(\theta\right)\quad;\quad dy=R.\cos\left(\theta\right).d\theta

Je te laisse effectuer les calculs. Tu vas obtenir une expression de la circulation élémentaire de la forme :

dC=f\left(\theta\right).d\theta

Si le théorème de Stokes est bien vérifié, tu devrais obtenir :

C=\intop_{0}^{2\pi}f\left(\theta\right).d\theta=3\pi R^{2}

Posté par
vanoisere : Rotationnel et divergence 08-10-21 à 14:36

Voici le schéma :

Rotationnel et divergence

Posté par
archange12re : Rotationnel et divergence 10-10-21 à 19:31

Bonjour (: , je vous remercie grandement ! le schéma m'a beaucoup aidé à comprendre!
Je vais m'attaquer à la partie 4, je reviens vers vous pour vous montrer ce que j'ai fais / vous demander de l'aide si j'en est besoin.

Posté par
archange12re : Rotationnel et divergence 11-10-21 à 09:47

Bonjour (:

Alors pour la question 4.1 j'ai déjà calculer la surface de chaque coté :
dS1 = p d theta dz
dS2 = p d p d theta
dS3 = d z d p

ensuite j'ai calculé le volume : dV = p d p d theta d z

Que dois je faire ensuite ? je ne suis pas sur que le calcul du volume sois nécessaire...

HS : Y a t il un problème avec l'affichage des formules sur le site ? je n'est plus les formules depuis hier d'écrit mais le texte écrit avec le Latex, j'ai donc préféré écrire les formules sans si vous avez le même problème

Rotationnel et divergence

Posté par
vanoisere : Rotationnel et divergence 11-10-21 à 11:49

Tu as réussi à terminer la question 3 ?
Pour 4 : il se trouve que j'ai démontré paragraphe 10 du document que je t'ai indiqué, la relation : dΦ=div(vec A).dV en utilisant les coordonnées cartésiennes. Tu peux t'inspirer de la méthode même si, ici, il faut utiliser les coordonnées cylindriques.
Ton schéma pose problème : si le centre C du volume élémentaire a pour coordonnées (,,z), l'arc MN est en (-d/2) et l'arc M'N' est en (+d/2). De même, MM' est en (-d/2) et NN' en (+d/2). Enfin : MM'NN' est en (z-dz/2) et QPP'Q' en (z+dz/2)
Tu as ensuite 6 vecteurs surface à exprimer...

Posté par
archange12re : Rotationnel et divergence 11-10-21 à 23:27

Pour la question 3 je pensais pouvoir réussir simplement le calcul mais je n'arrive pas a trouver 3pi R^2 , pouvez vous m'aider ?

Pour la question 4, je ne comprend pas trop, à quoi sert les 6 vecteurs surfaces, ce ne sont pas dS1, dS2 et dS3 ?

Posté par
vanoisere : Rotationnel et divergence 12-10-21 à 00:16

Pour 4 : il s'agit de calculer le flux élémentaire dΦ de \vec A à travers le volume élémentaire dV délimité par la surface fermée constituées des 6 faces du schéma. Puisque, selon le théorème d'Ostrogradski : dΦ=div(\vec A).dV, le calcul de dΦ et celui de dV permettent d'obtenir l'expression de div(\vec A) en coordonnées cylindriques.
Je t'aiderai demain pour finir la question 3.

Posté par
vanoisere : Rotationnel et divergence 12-10-21 à 15:04

Je reprends la question 3 en tenant compte de mon message du 08-10-21 à 14:29. On obtient :

dC=f(\theta).d\theta\quad avec\quad f(\theta)=-R^{3}.\cos\left(\theta\right).\sin^{2}\left(\theta\right)+\frac{1}{2}R^{3}.\cos^{3}\left(\theta\right)+3R^{2}.\cos^{2}\left(\theta\right)

Afin d'intégrer aisément, il faut faire disparaître de l'expression les carrés et les cubes en faisant intervenir les angles doubles et les angles triples. Sauf erreur de ma part, on obtient :

f(\theta)=\frac{1}{8}R^{3}.\cos\left(\theta\right)+\frac{3}{8}R^{3}.\cos\left(3\theta\right)+\frac{3}{2}R^{2}.\cos\left(2\theta\right)+\frac{3}{2}R^{2}

Il est très facile de démontrer :

\int_{0}^{2\pi}\left[\frac{1}{8}R^{3}.\cos\left(\theta\right)+\frac{3}{8}R^{3}.\cos\left(3\theta\right)+\frac{3}{2}R^{2}.\cos\left(2\theta\right)\right].d\theta=0

Donc :

C=\int_{0}^{2\pi}f(\theta).d\theta=\int_{0}^{2\pi}\frac{3}{2}R^{2}.d\theta=3\pi.R^{2}

Le théorème de Stokes est bien vérifié pour ce vecteur \overrightarrow{V} particulier.

Posté par
archange12re : Rotationnel et divergence 12-10-21 à 17:52

Bonjour (:

Je n'avais absolument pas pensé à utiliser les angles doubles ou les angles triples... J'ai refait le calcul et je tombe bien sur l'intégrale qui vaut C = 3\pi R^{2}. Cependant pour f\left(\theta \right) je ne trouve pas tout à fais la même chose, mais ce n'est pas très grave vu que j'arrive au même résultat final.


Je ne comprend pas pourquoi on cherche à déterminer div(A) pour la question 4.1

Posté par
vanoisere : Rotationnel et divergence 12-10-21 à 18:21

div\left(\overrightarrow{A}\right) a une expression simple en coordonnées cartésiennes mais la situation se complique en coordonnées cylindrique (voir formulaire en fin de mon document). Tu as ici une méthode possible de démonstration de l'expression de la divergence en coordonnées polaires.
La méthode consiste à calculer successivement le flux élémentaire à travers deux surfaces élémentaires opposées
1° : calculer dΦ1+dΦ'1 en fonction de dV et r et A et \frac{\partial A_{\rho}}{\partial\rho}
2° : calculer dΦ2+dΦ'2 en fonction de dV et \frac{\partial A_{z}}{\partial z}
3°:  calculer dΦ3+dΦ'3 en fonction de dV, r et \frac{\partial A_{\theta}}{\partial\theta}

Posté par
archange12re : Rotationnel et divergence 12-10-21 à 18:35

D'accord mais du coup cette démonstration est plus pour la question 4.2 ? je ne vois pas bien le lien avec le calcul du flux du vecteur A à travers la surface totale du volume élémentaire

Posté par
vanoisere : Rotationnel et divergence 12-10-21 à 18:49

Le flux total est la somme des six flux élémentaires définis dans mon message précédent et, selon le théorème d'Ostrogradski :

d\Phi=d\Phi_{1}+d\Phi'_{1}+d\Phi_{2}+d\Phi'_{2}+d\Phi_{3}+d\Phi'_{3}=div\left(\overrightarrow{A}\right).dV

L'expression du flux élémentaire total et celle du volume élémentaire permettent bien d'obtenir l'expression de la divergence...

Posté par
archange12re : Rotationnel et divergence 12-10-21 à 19:34

Ha d'accord, du coup il faut déja que je trouve les 6 six flux qui me permettront de trouver d\phi  ( c'est donc la reponse à la question 4.1) puis avec cela je peux donc trouver div(A).

Est ce bien cela ?

Posté par
vanoisere : Rotationnel et divergence 12-10-21 à 19:54

Oui !

Posté par
archange12re : Rotationnel et divergence 12-10-21 à 20:04

D'accord merci, je vais travailler sur ca se soir, je reviens vers vous demain matin (:

Posté par
vanoisere : Rotationnel et divergence 12-10-21 à 21:17

Je vais t'aider un peu pour le calcul des flux car cela n'a vraiment rien d'évident.Je vais faire le calcul pour le premier couple de surface puis je vais te laisser continuer...

On pose :

\overrightarrow{A}=A_{\rho}.\overrightarrow{u_{\rho}}+A_{\theta}.\overrightarrow{u_{\theta}}+A_{z}.\overrightarrow{u_{z}}

d\Phi_{1}+d\Phi'_{1}=\overrightarrow{A_{(\rho-\frac{d\rho}{2},\theta,z)}}.dS_{1}.\overrightarrow{u_{\rho}}+\overrightarrow{A_{(\rho+\frac{d\rho}{2},\theta,z)}}.dS'_{1}.\overrightarrow{u_{\rho}}

d\Phi_{1}+d\Phi'_{1}=-A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}.dz.\left(\rho-\frac{d\rho}{2}\right).d\theta+A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}.dz.\left(\rho+\frac{d\rho}{2}\right).d\theta

d\Phi_{1}+d\Phi'_{1}=\rho.d\theta.dz.\left[A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}-A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}\right]+d\theta.dz.\frac{d\rho}{2}\left[A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}-A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}\right]

Maintenant, il faut réfléchir avec à l'esprit que l'on raisonne sur les variations infinitésimales.

entre et +d, la composante A varie de façon pratiquement affine en fonction de  . On peut aussi imaginer un développement de Taylor limité au premier ordre...

\\ A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}-A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}=2A_{\rho(\rho,\theta,z)}

La différence entre le premier crochet correspond à la variation élémentaire de A quande varie de d. Il s'agit d'une différentielle :

A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}-A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}=\frac{\partial A_{\rho}}{\partial\rho}\cdot d\rho

Finalement,connaissant l'expression de dV :

d\Phi_{1}+d\Phi'_{1}=\left[\frac{\partial A_{\rho}}{\partial\rho}+\frac{A_{\rho}}{\rho}\right].dV=\frac{1}{\rho}\cdot\frac{\partial\left(\rho.A_{\rho}\right)}{\partial\rho}\cdot dV

Posté par
archange12re : Rotationnel et divergence 13-10-21 à 10:59

Bonjour,

J'avoue avoir un peu de mal avec les 2 lignes de calculs de d\phi 1 + d\phi' 1, je ne comprend pas comment vous êtes passé de la première ligne a la seconde puis a la troisième

Posté par
archange12re : Rotationnel et divergence 13-10-21 à 11:32

Juste pour être sur, lorsque je fais la dérivé partielle en x de :
exp(i(kx\bullet x + ky\bullet y + kz\bullet z))

On obtient bien :
kx * exp(i(kx\bullet x + ky\bullet y + kz\bullet z)) ?

Posté par
vanoisere : Rotationnel et divergence 13-10-21 à 12:49

Pour ne rien arranger, j'ai commis une erreur de signe en recopiant sous Tex la formule n°2 . Pour le calcul de dΦ1, le vecteur surface est orienté vers l'extérieur du volume donc suivant -\vec{u_\rho}. Je rectifie. Heureusement, cela n'impacte pas la suite qui prend bien en compte le signe "-".

\\ d\Phi_{1}+d\Phi'_{1}=-\overrightarrow{A_{(\rho-\frac{d\rho}{2},\theta,z)}}.dS_{1}.\overrightarrow{u_{\rho}}+\overrightarrow{A_{(\rho+\frac{d\rho}{2},\theta,z)}}.dS'_{1}.\overrightarrow{u_{\rho}}
dΦ1 est donc l'opposé du produit de la surface dS1 par la composante A du vecteur \vec A, composante calculée au point de coordonnée (-d/2,,z)
Même logique pour la suite.

Posté par
vanoisere : Rotationnel et divergence 13-10-21 à 15:34

Une autre faute de signe :

d\Phi_{1}+d\Phi'_{1}=\rho.d\theta.dz.\left[A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}-A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}\right]+d\theta.dz.\frac{d\rho}{2}\left[A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}+A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}\right]

Maintenant, il faut réfléchir avec à l'esprit que l'on raisonne sur les variations infinitésimales.

entre et +d, la composante A varie de façon pratiquement affine en fonction de  . On peut aussi imaginer un développement de Taylor limité au premier ordre...

\\ A_{\rho(\rho+\frac{d\rho}{2},\theta,z)}+A_{\rho(\rho-\frac{d\rho}{2},\theta,z)}=2A_{\rho(\rho,\theta,z)}

Posté par
archange12re : Rotationnel et divergence 13-10-21 à 21:15

J'ai essayé de faire pareil que vous mais pour $d\phi_{2}$ + $d\phi_{2}$'

$d\phi_{2}$ + $d\phi_{2}$' = $-A_{(\rho ,\theta ,z-dz/2)}$ $dS_{2}$ $u_{z}$ + $A_{(\rho ,\theta ,z+dz/2)}$ $dS_{2}$' $u_{z}$
$d\phi_{2}$ + $d\phi_{2}$' = $-A_{z*(\rho ,\theta ,z-dz/2)}$ *(z-dz/2) $d_{z}$ $d_{\theta }$ + $A_{z*(\rho ,\theta ,z+dz/2)}$ *(z+dz/2) $d_{z}$ $d_{\theta }$

Est ce que cela vous semble déjà correcte ?

Posté par
archange12re : Rotationnel et divergence 13-10-21 à 22:08

Je crois mettre trompé pour la seconde ligne c'est :

$d\phi_{2}$ + $d\phi_{2}$' = $-A_{z*(\rho ,\theta ,z-dz/2)}$ $d_{z}$ $d_{\theta }$ + $A_{z*(\rho ,\theta ,z+dz/2)}$ $d_{z}$ $d_{\theta }$

Posté par
vanoisere : Rotationnel et divergence 13-10-21 à 23:27

C'est bon. Il te reste juste à réaliser que \left[\ensuremath{-A_{z*(\rho,\theta,z-dz/2)}}+\ensuremath{A_{z*(\rho,\theta,z+dz/2)}}\right] représente la variation de Az quand z varie de dz. Il s'agit donc d'une différentielle. Le problème est effectivement plus simple que le premier cas que j'ai traité car ici, les aires élémentaires dS2 et dS'2 sont égales.

Posté par
archange12re : Rotationnel et divergence 14-10-21 à 00:32

Du coup je trouve :

$d\phi_{ 2}$ + $d\phi'_{ 2}$ = (d$A_{ z}$ / $d{ z }$ ) $d{ z }$ $d{ \theta }$ = (d$A_{ z }$ / $d{z }$ * \rho *$d{rho }$) dV


et

$d\phi_ {3}$ + $d\phi_ {3}$ ' = -$A_ {(\rho ,\theta-d\theta/2 ,z)}$ dS3 $u_ {\theta }$ + $A_ {(\rho ,\theta+d\theta/2 ,z)}$ dS3' $u_ {\theta }$

$d\phi_ {3}$ + $d\phi_ {3}$ ' = -$A_ {\theta (\rho ,\theta-d\theta/2 ,z)}$ $d_ {\rho }$ $d_ {\theta }$ + $A_ {\theta (\rho ,\theta+d\theta/2 ,z)}$ $d_ {\rho }$ $d_ {\theta }$

$d\phi_{ 3}$ + $d\phi'_{ 3}$ = (d$A_{ \theta }$ / $d{ \theta }$ ) $d{ \rho }$ $d{ \theta }$ = (d$A_{ \theta }$ / $d{ \theta }$ * \rho *$d{ z }$) dV


Est ce correct ?

Posté par
archange12re : Rotationnel et divergence 14-10-21 à 10:04

Donc pour la question 4.2 lorsque j'ai tous les d\phi je calcul d\phi puis grace au théorème de Green-Ostrogradsky j'ai :

\vec{div}(\vec{A}) = d\phi /dV

et

dV = \rho d\rho d\theta dz

Donc je trouve la divergence de A.

Pouvez vous aussi m'aider pour les question 4.3 et 4.4 s'il vous plait ?

Posté par
vanoisere : Rotationnel et divergence 14-10-21 à 11:18

Tu as quelques problèmes d'homogénéité dans tes formules :
dS2=dS'2=.d.d
dS3=dS'3=d.dz
Concernant l'expression de la divergence, tu peux t'autocorriger à partir du formulaire fourni en annexe du document déjà indiqué.
Pour les questions suivantes, il s'agit d'utiliser une méthode analogue pour le rotationnel. J'ai traité le problème paragraphe 13 du document en utilisant les coordonnées cartésiennes. Il faut adapter.
Pour chacun des trois contours définis par l'énoncé, il faut exprimer la circulation élémentaire dC du vecteur \vec A. En  écrivant ensuite : dC=\overrightarrow{rot}\left(\overrightarrow{A}\right).\overrightarrow{dS} pour chacun des trois contours, tu vas obtenir les trois composantes du vecteur rotationnel.

Posté par
archange12re : Rotationnel et divergence 14-10-21 à 11:31

Je ne vois pas trop comment vous avez trouvez les surfaces dS2 et dS3 avec les notations du schéma pour moi dS3 = d\rho * d\theta.

Je suis désolé mais je ne comprend pas comment faire pour la question 4.3, j'ai bien compris qu'il fallait calculer dC pour chaque contour mais je ne comprend pas trop la méthode.
Je suis d'accord lorsque j'aurais dC il sera simple d'obtenir rot(A) (cela ressemble un peu à la question 4.2 finalement).

Posté par
vanoisere : Rotationnel et divergence 14-10-21 à 11:55

Citation :
dS3 = d\rho * d\theta.

Nécessairement faux car non homogène. N'oublie pas qu'un angle, exprimé en radian, est une grandeur de dimension "1", grandeur "sans dimension" comme on dit aussi parfois. En effet un angle exprimé en radian est toujours défini comme le rapport de deux longueurs (revois au besoin ton cours de math sur le sujet.
Bref : tu est en train d'écrire que l'aire d'une surface (dS3) est égale à une longueur ! ! !
Comme je l'ai déjà écrit :
MN=(-d/2).d
M'N'=(+d/2).d

dS_{3}=dS'_{3}=MM'\cdot\frac{MN+M'N'}{2}=\rho.d\rho.d\theta

Posté par
archange12re : Rotationnel et divergence 14-10-21 à 20:22

ha oui d'accord je m'étais trompé dans le calcul.

Pouvez vous m'aider un peu plus pour la question 4.3 s'il vous plait?

Posté par
vanoisere : Rotationnel et divergence 14-10-21 à 20:57

Tu calcules la circulation élémentaire dC sur le parcours fermé M'N'P'Q' puis tu appliques le théorème de Stokes :
dC=\overrightarrow{rot}\left(\overrightarrow{A}\right).dS'_{1}.\overrightarrow{u_{\rho}}
Cela va te fournir la composante du rotationnel suivant \overrightarrow{u_{\rho}}
Tu obtiens les deux autres composantes du rotationnel en t'intéressant aux deux autres circuits fermés proposés par l'énoncé.
As-tu lu et compris le paragraphe 13 du document déjà fourni ?

Posté par
archange12re : Rotationnel et divergence 14-10-21 à 21:24

D'accord je dois donc calculer dL mais ce n'est pas comme dans la question 3, on avait un vecteur V, comment suis je censé faire ?

J'ai essayé :
\vec{dC} = \vec{A}.\vec{dl} = $A{x}$.$d{x}$ + $A{y}$.$d{y}$
Mais après on ne connais pas Ax et Ay comment dois je faire ?

Posté par
vanoisere : Rotationnel et divergence 14-10-21 à 21:58

Attention  : dC est un produit scalaire, pas un vecteur. C'est une somme de 4 produits scalaires.  En les sommant deux à deux, il est possible de faire apparaître deux différentielles qui font apparaître des dérivées partielles comme dans le raisonnement précédent sur la divergence.

Posté par
archange12re : Rotationnel et divergence 14-10-21 à 23:29

Oui pour la flèche de dC c'est une erreur de ma part, j'ai étais trop vite.

Par contre je ne comprend pas de quelle somme vous parlez, quels sont ses 4 produits scalaires ?

Posté par
vanoisere : Rotationnel et divergence 15-10-21 à 12:25

Revois dans ton cours ou à défaut sur mon document la notion de circulation d'un vecteur le long d'un contour fermé. Remarque par rapport à l'énoncé : puisqu'il s'agit d'établir l'expression de \overrightarrow{rot}\left(\overrightarrow{A}\right) au point de coordonnées (,,z), contrairement à ce que suggère ton énoncé, il faut choisir un contour fermé élémentaire dans un plan contenant le point de coordonnées (,,z),  Je suggère le contour ABCD du schéma ci-dessous. La circulation est bien une somme de 4 termes :

\overrightarrow{AB}.\overrightarrow{A_{\left(\rho-d\rho/2,\theta,z\right)}}+\overrightarrow{BC}.\overrightarrow{A_{\left(\rho,\theta-d\theta/2,z\right)}}+\overrightarrow{CD}.\overrightarrow{A_{\left(\rho+d\rho/2,\theta,z\right)}}+\overrightarrow{DA}.\overrightarrow{A_{\left(\rho,\theta+d\theta/2,z\right)}}

Rotationnel et divergence

Posté par
archange12re : Rotationnel et divergence 17-10-21 à 21:10

Bonsoir,

Si je comprend bien, pour déterminer la circulation du vecteur A le long du trajet orienté M'N'P'Q' , je dois faire :

M'N'.$A_{(\rho +d\rho /2,\theta ,z)} $ + N'P'.$A_{(\rho,\theta ,z+dz/2)}$ + P'Q'.$A_{(\rho - d\rho/2 ,\theta ,z)}$ +Q'M'.$A_{(\rho,\theta ,z-dz/2)}$

Ce sont bien des vecteurs, je n'ai juste pas réussis à mettre les flèches correctement ...

Je vois bien qu'il y a 2 A avec rho et d rho /2 et qu'il y a 2 A avec z et dz/2, comme à la question 4.1.
Cependant je ne sais pas comment faire apparaitre les différentiels et après les avoir obtenus que suis censé faire ?  

Posté par
vanoisere : Rotationnel et divergence 18-10-21 à 13:16

Je veux bien t'aider à trouver la composante du rotationnel suivant (Oz). Je te laisserai trouver les deux autres. Je reprends les notations de mon précédent message en regroupant les termes par deux comme fait lors de l'étude de la divergence.

\overrightarrow{AB}.\overrightarrow{A_{\left(\rho-d\rho/2,\theta,z\right)}}+\overrightarrow{CD}.\overrightarrow{A_{\left(\rho+d\rho/2,\theta,z\right)}}=-\left(\rho-\frac{d\rho}{2}\right)d\theta.A_{\theta(\rho-d\rho/2,\theta,z)}+\left(\rho+\frac{d\rho}{2}\right)d\theta.A_{\theta(\rho+d\rho/2,\theta,z)} \\
\overrightarrow{AB}.\overrightarrow{A_{\left(\rho-d\rho/2,\theta,z\right)}}+\overrightarrow{CD}.\overrightarrow{A_{\left(\rho+d\rho/2,\theta,z\right)}}=\rho.d\theta.\left[A_{\theta(\rho+d\rho/2,\theta,z)}-A_{\theta(\rho-d\rho/2,\theta,z)}\right]+\frac{d\rho}{2}\left[A_{\theta(\rho-d\rho/2,\theta,z)}+A_{\theta(\rho+d\rho/2,\theta,z)}\right].d\theta

\overrightarrow{AB}.\overrightarrow{A_{\left(\rho-d\rho/2,\theta,z\right)}}+\overrightarrow{CD}.\overrightarrow{A_{\left(\rho+d\rho/2,\theta,z\right)}}=\rho.d\theta.\left(\frac{\partial A_{\theta}}{\partial\rho}\right).d\rho+A_{\theta(\rho,\theta,z)}.d\rho.d\theta

Les justifications ont été fournies lors de l'étude de la divergence.

\overrightarrow{BC}.\overrightarrow{A_{\left(\rho,\theta-d\theta/2,z\right)}}+\overrightarrow{DA}.\overrightarrow{A_{\left(\rho,\theta+d\theta/2,z\right)}}=d\rho.A_{\rho(\rho,\theta-d\theta/2,z)}-d\rho.A_{\rho(\rho,\theta+d\theta/2,z)}

\overrightarrow{BC}.\overrightarrow{A_{\left(\rho,\theta-d\theta/2,z\right)}}+\overrightarrow{DA}.\overrightarrow{A_{\left(\rho,\theta+d\theta/2,z\right)}}=-\frac{\partial A_{\rho}}{\partial\theta}d\rho.d\theta

D'où l'expression de la circulation élémentaire sur le circuit fermé (ABCD) :

dC_{3}=\left[\frac{A_{\theta}}{\rho}+\frac{\partial A_{\theta}}{\partial\rho}-\frac{1}{\rho}\frac{\partial A_{\rho}}{\partial\rho}\right].\rho.d\rho.d\theta

Or, selon le théorème de Stokes, la surface associée à ce contour est :

\overrightarrow{dS_{3}}=\rho.d\rho.d\theta.\overrightarrow{u_{z}}

avec :

dC_{3}=\overrightarrow{rot}\left(\overrightarrow{A}\right).\overrightarrow{dS_{3}}

Par identification :

\overrightarrow{rot}\left(\overrightarrow{A}\right).\overrightarrow{u_{z}}=\frac{A_{\theta}}{\rho}+\frac{\partial A_{\theta}}{\partial\rho}-\frac{1}{\rho}\frac{\partial A_{\rho}}{\partial\rho}

Tu obtiens ainsi la composante du rotationnel selon l'axe (Oz) :

\left[\overrightarrow{rot}\left(\overrightarrow{A}\right)\right]_{z}=\dfrac{1}{\rho}\cdot\left[\dfrac{\partial\left(\rho\cdot A_{\theta}\right)}{\partial\rho}-\dfrac{\partial A_{\rho}}{\partial\theta}\right]

Reste maintenant à déterminer les circulations élémentaires dC1 et dC2 pour obtenir les deux autres composantes du rotationnel.

Posté par
archange12re : Rotationnel et divergence 20-10-21 à 12:06

Je vous remercie (:


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !