Rotation d'une section (résistance des matériaux), exercice de Physique

 Niveau maths spéPartager :
			        
Rotation d'une section (résistance des matériaux)
Posté par 
physrela  22-03-15 à 13:59
Bonjour, 

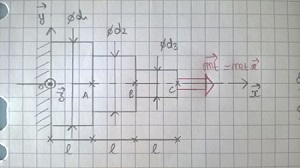
J'ai un exercice sur la torsion que je n'arrive pas à résoudre. On me demande de déterminer la rotation de la section en C. Je ne vois pas comment m'y prendre. 

 Posté par 
gbm re : Rotation d'une section (résistance des matériaux)  22-03-15 à 15:15
Salut, 

Tu as très certainement vu une formule apte à t'aider ici non ?
 Posté par 
physrelare : Rotation d'une section (résistance des matériaux)  22-03-15 à 15:21
J'ai plusieurs formules. Notamment =G avec  la contrainte tangentielle, G le module de Coulomb, l'angle unitaire de torsion et  le rayon de la section et j'ai une autre formule qui donne mt=GI0 avec I0 le moment quadratique polaire. 
 Posté par 
gbm re : Rotation d'une section (résistance des matériaux)  22-03-15 à 15:59
Bah alors, tu ne peux pas exploiter ces formules ?

 Posté par 
physrelare : Rotation d'une section (résistance des matériaux)  22-03-15 à 16:24
Je ne vois pas quoi faire vu qu'il y a trois diamètres différents
 Posté par 
gbm re : Rotation d'une section (résistance des matériaux)  22-03-15 à 17:30
Alors, 

La déformation angulaire en torsion  d'un arbre entre deux points d'abscisse  et  vaut pour rappel :

 moment quadratique polaire

 module d'élasticité transversale.

Donc pour un arbre cylindrique à section constante de longueur  :

Pour un arbre cylindrique avec épaulements, on aura :

En d'autres termes, tu discrétises .
 Posté par 
gbm re : Rotation d'une section (résistance des matériaux)  22-03-15 à 17:31
Est-ce plus clair pour toi à présent  ?
 Posté par 
physrelare : Rotation d'une section (résistance des matériaux)  22-03-15 à 18:16
Oui c'est très clair. En fait on prend chaque section séparée puis on somme. 
 Posté par 
gbm re : Rotation d'une section (résistance des matériaux)  22-03-15 à 18:19
C'était le plus simple n'est-il point  ?
 Posté par 
physrelare : Rotation d'une section (résistance des matériaux)  22-03-15 à 18:55
Oui c'est exact  En tout cas merci beaucoup et à une prochaine 
  Posté par 
gbm re : Rotation d'une section (résistance des matériaux)  23-03-15 à 07:56
De rien 

A+