Inscription / Connexion Nouveau Sujet
Rotation autour d'un axe, force de coriolis..
Bonsoir à tous,
Je bloque sur cet exo :
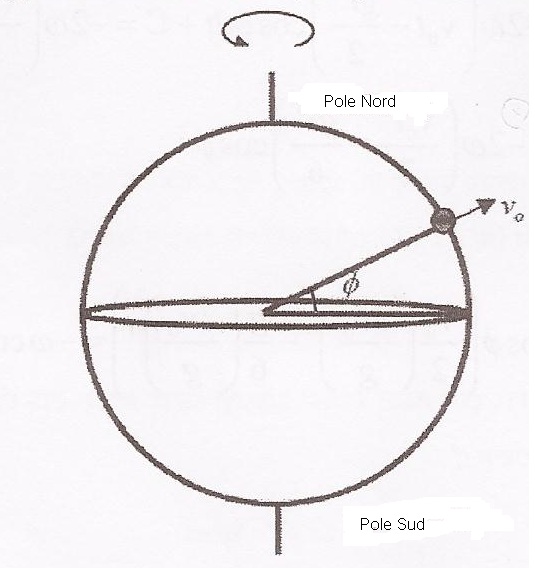
Un corps est lancé depuis le sol à une latitude 
au nord. La vitesse de lancé est V0, et elle est petite, de telle sorte que l'on puisse supposer g constant dans le sens contraire au sens de lancé.La fréquence de rotation de la terre est 
.
Quelle est la distance que le corps lancé a parcouru depuis l'endroit de lancé jusqu'à l'endroit où il tombera à cause de la force de coriolis ?
Attention : au point où est dessiné le corps, la direction ouest est dirigée en dehors de la feuille (vers nous).
Je sais qu'il faut commencer par écrire l'accélération de coriolis, mais le problème c'est pour exprimer la vitesse en fonction de Vy etc.. Je débute sur ce chapitre et j'avoue que ce n'est pas très clair (pas très simple aussi !). Si quelqu'un pouvez m'aider ça serait super.
Merci d'avance ! 
bonjour,
pour cet exo il faut remarquer que l'accélération de Coriolis est très faible sur terre si Vo est "petit"
en effet 
c = 2
^ Vr donc |c| <= | 2 Vr |
comme | 2 | 
1,5 10-4
pour de faibles vitesses on trouve donc une accélération de Coriolis très faible par rapport à g
tu peux donc considérer que le mouvement est une chute libre verticale (z"=-g, z'=Vo-gt), puis calculer ensuite Fc en estimant que v est dirigée selon la verticale (on ne retient que z' car on néglige les autres composantes dues à Coriolis et donc très faibles). Tu vas trouver une force Fc dirigée selon l'axe est-ouest et en projetant la relation fondamentale sur cet axe tu trouves la déviation demandée (après intégration)
Salut,
Merci pour ta réponse,
Ok je saisis un peu mieux, mais pourrais-tu m'expliquer ce que ceci signifie : (tiré de la correction de l'exo).
Calcul de l'accélération de coriolis :
acor = -2
= -2Vysin(90-)x
J'ai du mal à comprendre ce qu'est cette composante de Vy, comment la voir ?
Merci d'avance.
bonjour,
Fc = - mc = -2m ^ V
en prenant comme repère (Oxyz) avec O point de départ
(Ox) orienté vers l'est (vecteur dir. 
)
(Oy) vers le nord (vecteur dir. 
)
(Oz) verticale passant O orientée positivement vers le haut (vecteur dir. 
= ^ )
à t=0, M est en O et z'o = Vo
en écrivant que v est verticale donc v = z'
et que
= cos + sin
le produit vectoriel donne: ^ v = z'cos
d'où Fc = -2mz'cos
et comme z' = Vo - gt on trouve finalement en projetant la loi fondamentale sur (Ox)
mx" = -2mcos (Vo - gt)
sauf erreur
Annuler
connectez vous