Niveau maths sup

Ressort en série

Posté par
Kai22 10-09-16 à 18:53

Bonjour.

Je dois trouver l'expression de la constante de raideur K d'un unique ressort équivalent à deux ressorts de raideur k1 et k2 placés en série (j'ai fait un dessin : à gauche, je mets le ressort 1 et à droite je lui attache le ressort 2 au bout duquel est accroché une masse m).
Je bloque un peu mais je vous expose déjà ce que j'ai fait :

Système : {masse m}
Référentiel : supposé galiléen
Bilan des force sur le système :
- poids et réaction du support mais je ne les prends pas en compte dans l'étude car les deux se compensent
- la force élastique F2 émanant du ressort 2

On écrit la loi de Hooke (les axes que j'ai choisis : Ox horizontal vers la droite et Oz vertical vers le haut mais on ne s'occupe pas des ordonnés en fin de compte).
F2 = -k2(x-l02) avec l02 la longueur à vide du ressort 2

De même j'établis la loi de Hooke pour le ressort 1 :
F1 = k1(x-l01) (notations analogues à celles ci-dessus)

Et ensuite, je fais quoi ?!

Pouvez-vous m'aider ? Merci par avance !

Posté par re : Ressort en série 10-09-16 à 19:11

Bonsoir
ce problème a déjà été évoqué sur ce forum ici : Ressorts équivalents à une association série et parallèle

Posté par re : Ressort en série 10-09-16 à 23:33

J'ai déjà vu cela en effet, mais je ne comprends pas les histoires de ressort à l'équilibre.

Posté par re : Ressort en série 11-09-16 à 15:10

Bonjour
La démonstration faite par gbm me parait claire et rigoureuse... Je veux bien tenter une autre approche qui ne sera pas, de toutes façons, fondamentalement différente.
Tu as besoin au préalable de connaître deux lois de la physique :
1° le principe des actions réciproques (principe de l'action et de la réaction) : si un corps 1 exerce sur un corps 2 une force $\overrightarrow{F_{12}}$ , le corps 2 exerce sur le corps 1 au même instant une force $\overrightarrow{F_{21}}$ égale à $-\overrightarrow{F_{12}}$ .
2° le principe fondamental de la dynamique (seconde loi de Newton). Je ne développe pas à ce niveau...

Je considère deux ressorts 1 et 2 de masses d'influence négligeable, de constantes de raideurs respectives k₁et k₂ et je cherche la constante de raideur k du ressort équivalent (voir schéma ci-dessous). L'association série des deux ressorts est soumise à une force de traction $\vec{F}$ . Le ressort équivalent subit un allongement l tel que : F = k.l.
Le ressort 2, soumis à la force $\vec{F}$ à son extrémité inférieure subit un allongement l₂ tel que F=k₂.l₂.
Appliquons maintenant la seconde loi de Newton au ressort n°2 :
Les actions extérieures sont :
La force exercée par le ressort 1 : $\vec{F_{12}}$
Le poids du ressort : $m_2\cdot\vec{g}$
La force de traction $\vec{F}$
Cela donne :

$\overrightarrow{F_{12}}+m_{2}\cdot\overrightarrow{g}+\overrightarrow{F}=m_{2}\cdot\overrightarrow{a_{G2}}$
(accélération du centre d'inertie G₂ du ressort 2)
En posant : m₂=0, on obtient :

$\overrightarrow{F_{12}}+\overrightarrow{F}=\overrightarrow{0}$
La force exercée par le ressort 2 sur le ressort 1 est, par application du principe des actions réciproques :

$\overrightarrow{F_{21}}=-\overrightarrow{F_{12}}=\overrightarrow{F}$
Donc : F₂₁=k₁.l₁=F
En faisant la synthèse, on obtient :

$F=k\cdot\triangle l=k_{2}\cdot\triangle l_{2}=k_{1}\cdot\triangle l_{1}$
Puisque, évidemment : l=l₁+l₂ :

$\frac{F}{k}=\frac{F}{k_{1}}+\frac{F}{k_{2}}$
Puisque : F0, on obtient le résultat :

$\frac{1}{k}=\frac{1}{k_{1}}+\frac{1}{k_{2}}$
Comme précisé déjà par gbm, il y a une analogie forte avec l'association de condensateurs...

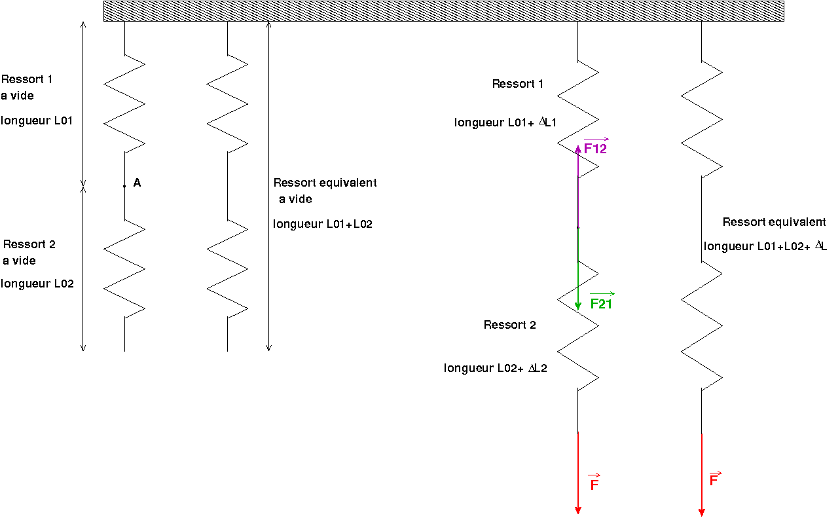
Ressort en série

Posté par re : Ressort en série 11-09-16 à 18:36

Dans mon schéma, je n'avais pas placé les ressorts à la verticale, de sorte que le poids de ceux-ci n'était pas à prendre en compte. Mais puisque vous mettez que m2=0 alors j'imagine que ça revient au même.
La force F s'applique-t-elle également dans le cas des ressorts horizontaux ?

Posté par re : Ressort en série 11-09-16 à 18:57

À partir du moment où il est possible de considérer comme négligeable l'influence des masses des ressorts, la démonstration est valide quelle que soit l'orientation des ressorts dans l'espace. La force de vecteur $\vec{F}$ doit être colinéaire à l'axe des ressorts.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Ressort en série

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique