Inscription / Connexion Nouveau Sujet
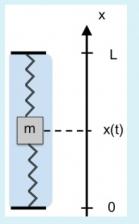
ressort
Bonjour,
cela fait 2 jours que j'essai de trouver les réponses mais je n'y arrive pas...
auriez vous une piste?
Merci par avance pour votre aide.
(suite de l'image)
k=100 N.m-1
L0=0,3 m
μ= 8,1 SI
L=1 m
x0 =x(t=0) = 0,42 m
g=10 m.s-2
La solution de l'équation différentielle du mouvement de la masse est la suivante :
Les 4 questions suivantes demandent les valeurs numériques de respectivement A, B, C et D (en SI).
Bonsoir
Les questions ne sont pas posées. Le problème se traite comme s'il n'y avait qu'un seul ressort de raideur 2k.
Poste l'énoncé intégral puis indique ce que tu as fait et ce qui te bloque exactement.
Merci d'avoir fait remonter cet oubli.
voici ce qu il manque.
Encore merci pour ton aide.
** image supprimée **
Attention : le règlement du forum demande de scanner les schémas mais de recopier les énoncés.
Si je comprends bien, il s'agit d'exprimer en fonction des caractéristiques du montage et des conditions initiales, les constantes A, B, C et D ?
D est la valeurs de x à l'équilibre .
A et B s'obtiennent à partir de la position initiale et de la valeur initiale. La constante C se déduit de l'équation différentielle vérifiée par x.
Je te laisse travailler et proposer des solutions. Pose des questions précises si nécessaire sur ce que tu ne comprends pas.


