Bonjour
On démontre en math que la solution générale à cette équation différentielle est une somme de deux termes :
- La solution particulière correspondant au cas où la dérivée par rapport à t est nulle.
cette solution est bien égale à -g.T
- la solution correspondant à la constante nulle, soit la solution de l'équation différentielle : dv/dt)+(1/T)v=0 ; cette solution est A.exp(-t/T). La solution générale est donc ainsi :
v=A.exp(-t/T) -g.T
Tu détermines la valeur de la constante A à partir du cas particulier de l'instant initial.
La méthode générale d'obtention de la trajectoire a été exposé sur ce forum il y a peu ici :
Calcul d'une vitesse initiale

Merci
C'est justement là que je bloque, je ne comprends pas la méthode pour déterminer A avec les conditions initiales.

Je ne peux pas dire que v0= A - gT = 0  et donc A = gT car on est justement censé trouver v0.. ou pas?

Merci pour le lien

Une fois établie l'équation différentielle vectorielle déduite de la relation fondamentale de la dynamique, la projection de cette relation dans un repère (Oxz) où O est la position initiale du centre du ballon, où (Ox) est l'axe horizontal et (Oz) l'axe verticale ascendant (voir lien fourni), conduit à deux équations différentielles qui concernent les composantes du vecteur vitesse sur les deux axes :





Comme déjà expliqué, la solution de la première est :



Tu obtiens A en remarquant qu'à la date t = 0 :



La seconde équation différentielle admet comme solution générale :



Tu obtiens B en remarquant qu'à la date t=0 :



Une fois obtenues les expression des deux composantes de la vitesse, une intégration par rapport à t va permettre d'obtenir les coordonnées du centre du ballon (x,z).

Bonjour,

Merci pour votre réponse, désolé pour le retard, je n'ai pas pu vous répondre avant.
Je ne sais toujours pas comment trouver les constantes A et B.
J'ai trouvé selon uz : v(t) = Aexp(-t/T)-gT et donc v(t=0)= A-gT+vosin(alpha)
selon ux : v(t) =  (-1/T)Bexp(-t/T) et donc v(t=0)=(-1/T)B = vocos(alpha)

Pourriez-vous m'éclairer s'il vous plait ?

Tu y es presque !





D'où les expressions des deux composantes du vecteur vitesse :





Il te reste à intégrer ces deux expressions par rapport au temps pour obtenir les coordonnées (x,z) du centre du ballon.

D'accord, mais comment trouver v0 à partir de ces 2 formules. Nous avons 2 équations, 2 inconnues mais elles sont assez compliquées à résoudre.

Il faut intégrer pour obtenir x = f(t) et z=g(t) puis écrire que si x=56m, z=26m.
Je suppose que 26m désigne l'altitude du panier par rapport à la position de lancer. S'il s'agit de l'altitude par rapport au sol, il faudrait aussi connaitre l'altitude de départ que tu n'indiques pas.

En primitivant vx(t) pour avoir x(t) j'obtient : x(t) = -vo.cos(alpha).T.(exp(-t/T))
On a z0=0 et x0=0
Si j'écrit que x(t=0)=0, on a v0cos(alpha)T=0 et donc v0=0
Je crois que je me perds dans mon raisonnement ou alors je me suis trompée dans l'intégration..

En intégrant par rapport à t, on obtient :





où C et D sont deux constantes qui se déterminent en considérant que xo=0 et zo=0. Je t'ai indiqué la méthode pour obtenir Vo . Cela suppose de connaître qui se détermine en fonction de la masse m du ballon et de la constante de la force de frottement que tu n'as pas indiquée...

Ah oui, T = m/lambda avec m= 1kg et lambda = 0,01kg/s

Du coup j'isole t final (tf) et j'obtient :

tf = -Tln(600/(-100Vocos(65))
Et j'injecte ce tf dans l'expression de z.
J'ai ensuite une equation très longue et compliquée à résoudre, comment faire ?

J'ai 1 équation, 1 inconnue :

26 = -T(Vosin(alpha)(56/(-100Vocos(alpha))+gT(Tln(56/(-100Vocos(alpha))))

Que vient faire l'angle de 65° ? tu as indiqué précédemment : =40° ???
Tu as aussi : = 100s.



La date t1 d'entrée dans le panier vérifie :



Cela te donne une relation entre t1 et Vo. Tu injectes cette expression de t1 dans l'équation donnant z : cela te donne une équation à une seule inconnue : Vo. Il faut reconnaître que cela est assez calculatoire. Il est peut-être possible de fournir uniquement une solution numérique plutôt que littérale...

Oui, je me suis trompé d'énoncé sur mon brouillon j'ai noté les valeurs du sujet dans le lien que vous m'aviez partagé.

Si je comprends bien votre constante C est égale à T*Vo*cos(alpha) et je ne comprends pas bien pourquoi parce que x0=0 donc C=0 ?

Et aussi angle = 40° par rapport à la verticale donc alpha = 90-40=50° non ?

Étourderie de ma part : =50° comme tu le dis dans ton dernier message.
Si on considère que la cible correspond à x=56m , il faut poser xo=0. Regarde de plus près les expressions de x et de z que j'ai fournies à 19h57. Elles correspondent bien à xo=0 et zo=0... N'oublie pas que exp(0)=1...

D'accord, merci

J'ai isolé t1 et j'ai trouvé t1 = -100ln(1-(56/100Vocos(50)))

Est-ce que jusque là c'est juste ?

En réinjectant ce t1 dans ma formule, j'ai v0=0,24 m/s, je ne sais pas du tout si l'erreur vient d'après ou de t1

J'obtiens :



La valeur de z correspondante à cette date t1 est :



Avec :



Une résolution numérique conduit à :



Voici le tracé de la trajectoire qui a l'allure d'une parabole dans la mesure où les frottements sont relativement faibles. Évidemment, cette modélisation, comme expliqué dans l'autre sujet, n'est pas très réaliste...

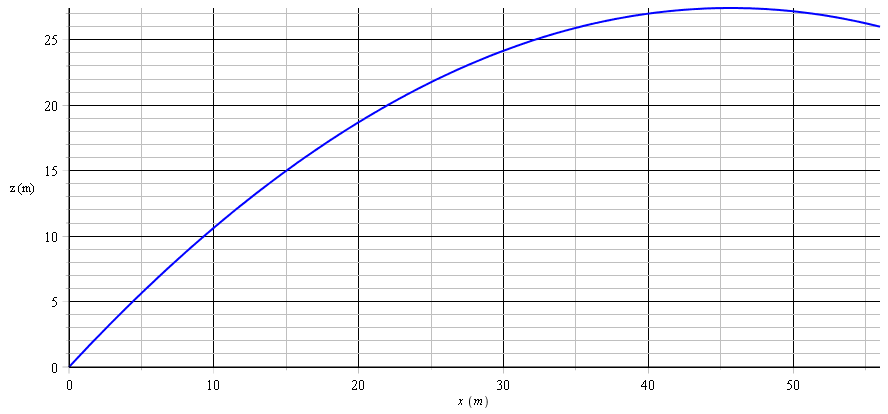
Est-ce que vous obtenez v0 grâce à une calculatrice graphique ? J'aimerai pouvoir essayer de résoudre ça sur un logiciel.

Merci beaucoup pour votre aide, j'ai tout compris et beaucoup appris

Il existe maintenant des calculatrices graphiques performantes et programmables ainsi que des calculatrices alphanumériques qui font certains calculs littéraux.
Personnellement, j'ai utilisé ici le logiciel Maple. Il permet les calculs littéraux , les applications numériques et les tracés de courbes. C'est un logiciel payant mais il existe des versions pour étudiants pas très chères.
Les ingénieurs utilisent beaucoup Matlab : c'est un logiciel très puissant pour la programmation et les calculs numériques. Il est très cher. SCILAB est un logiciel gratuit, presque aussi puissant que Matlab mais à l'interface moins ergonomique.

Je viens de reprendre l'exercice et dans l'expression de vx(t) nous avons cos(x) et dans celle de x(t) aussi, en primitivant, on aurait dû trouver un sinus ?

autant pour moi, cos est une constante