Inscription / Connexion Nouveau Sujet
Calcul d'une vitesse initiale
Bonjour, voilà je bloque je dois essayer de faire cet exercice mais je ne sais pas par où commencer:
Le but est de créer un robot capable de lancer un ballon de basket Ball depuis le trocadero jusqu'au 3 eme étage de la tour effel.
Le robot est situé à 600 m de la verticale de la tour effel z=0
Le troisième étage est à une hauteur de 276 mètres
L'angle de tir est de 25 degré par rapport à la verticale
La masse du ballon est de 1 kg
L'objectif est d'établir la vitesse initiale en fonction de 3 conditions de tir absence de frottement, lambda = 0'01kg/s et lambda =0.1 kg/s
Dois je appliquer le Ffd et enfin Pythagore pour pouvoir connaître la longueur de l'hypothèse je ne sais pas trop vu que la trajectoire du ballon n'est pas une ligne droite mais plutôt une parabole nan ?
Merci de m'éclaircir un peu 
Bonjour
Je veux bien t'indiquer la méthode générale puis te laisser travailler...
Tu choisis un repère lié à la terre (Oxz) contenant le vecteur vitesse initiale, O correspondant à la position initiale du centre du ballon, l(axe (Oz) étant vertical.
Tu poses les expressions de l'accélération :
Puis tu intègre deux fois par rapport au temps en tenant compte des conditions initiales :
x=...
z=...
Je ne sais pas si connais les notations « point » et « double point » pour désigner la dérivée et la dérivée seconde par rapport au temps. Dans le doute, j'ai utilisé les deux notations.
Tu peux ensuite calculer la date t correspondant à x=600m. Tu reportes dans l'expression de z en posant z=276m. Tu obtiens ainsi une équation avec une seule inconnue : vo.
Je te laisse travailler. Bien sûr : l'absence de frottement correspond au cas simple : ...
PS : ce problème n'est pas très réaliste : à de telles vitesses, pour un ballon aussi gros, la force de frottement exercée par l'air est plutôt proportionnelle au carré de la vitesse et non à la vitesse mais alors : les calculs sont beaucoup plus compliqués !
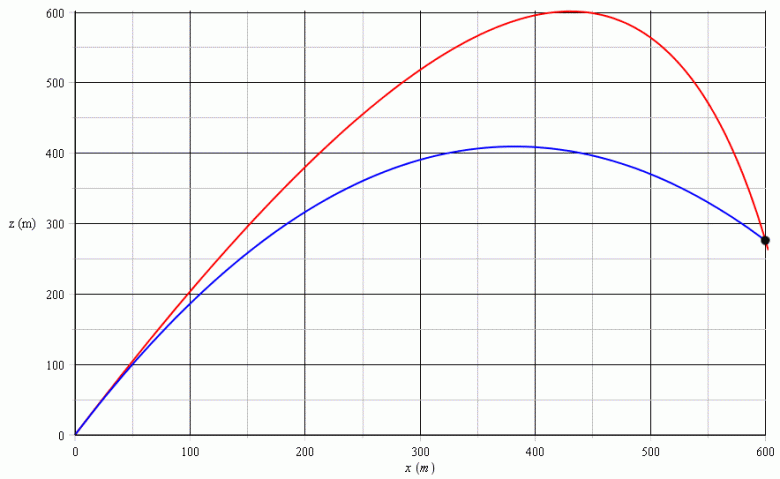
Les deux trajectoires simulées ci-dessous t'aideront à comprendre à quel point la trajectoire est éloignée d'une ligne droite ! En bleu la trajectoire parabolique correspondant à l'absence de frottement, en rouge la trajectoire correspondant à 
=0,1kg/s. Le point cible (600m,276m) est représenté par un petit disque noir.
Les deux trajectoires correspondent à des vecteurs vitesse initiale de normes différentes mais ayant même direction et même sens. Elles admettent donc une tangente en (0,0) commune.
Merci beaucoup d'avoir pris le temps pour répondre à mes questions. Je vais revoir tout cela ce soir.
Pour les 2 paraboles ça m'a beaucoup aidé à visualiser la trajectoire avec ou sans frottement.
Merci encore !
Bonne soirée
OK ! Bon courage !
Attention : la courbe bleue est bien une parabole mais pas la courbe rouge : les frottements compliquent la situation !
Par contre j'ai un petit soucis quand j'applique la deuxième loi de Newton
On a donc P+F =m.a
- mg-.v=ma Donc a(ou x secondes) = - g-. Z(dérivée)
Je ne trouve donc pas la même expression De l'accélération que vous :/
Ps 
ardon je n'ai pas réussi à trouvé comment faire les flèches pour vecteur
Annuler
connectez vous