Inscription / Connexion Nouveau Sujet
Résistance équivalente
Bonsoir tout le monde j'ai un petit problème sur la façon de chercher la résistance équivalente.Merci à tous ceux qui m'aideront. Voila le sujet: chaque trait représente une résistor de résistance R.Déterminer la résistance équivalente de ce réseau vu des points A et B.
oui exactement il y a 12 résistances.
Et je n'arrive pas à trouver la résistance équivalente. Pouvez-vous m'aider? J'en serai ravi.
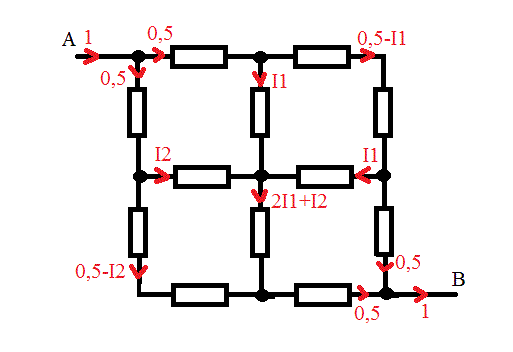
On injecte un courant d'1 ampère au point A (il y aura bien entendu ce même courant d'1 A qui "sortira" en B).
Par raison de symétrie, ce courant de 1 A se divise également entre les 2 branches qu'il rencontre --> 0,5 A dans chaque branche.
On complète les courants dans les autres branches en introduisant I1 et I2 ...
U(AB) = 0,5*R + 2R*(0,5-I1) + 0,5*R = 2R*(1 - I1)
U(AB) = 0,5*R + 2R*(0,5-I2) + 0,5*R = 2R*(1 - I2)
Et donc I1 = I2
U(AB) = 0,5*R + R*I1 + R*I2 + 0,5*R = R + 2R*I1
2R*(1 - I1) = R + 2R*I1
2*(1 - I1) = 1 + 2*I1
4I1 = 1
I1 = 0,25 A
U(AB) = 2R*(1 - 0,25) = 1,5.R
U(AB) = R(AB) * 1
--> R(AB) = 1,5.R
-----
Sauf distraction. 
Bonsoir j'ai encore un problème pour le calcul de la résistance équivalente d'un réseau. Aidez moi s'il vous plaît. Voila l'énoncé: On considère le réseau de résistances électriques suivant. Chaque côté a une résistance R.(autrement dit il y a 12 résistances puisqu'il y a 12 côtés)
1) Déterminer la résistance équivalente Rc1 vue entre les points A et B. (là on m'avait aidé et Rc1= )
2) Déterminer la résistance équivalente Rc2 vue entre les points A et C.
3) Déterminer la résistance équivalente Rc3 vue entre les points B et C.
(Les questions 2 et 3 je m'embrouille et je n'y arrive pas. Aidez moi s'il vous plaît).Merci et excusez moi pour mon mauvais art de la figure.
*** message déplacé ***
Comment sont connectées les résistances ?
Que sont ces " 12 côtés " ?
Où sont les points A, B et C ?
*** message déplacé ***
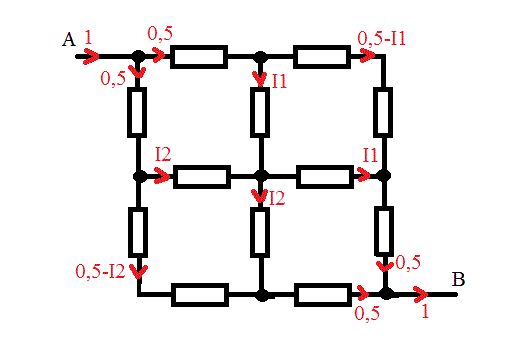
Voila le circuit.Là c'est pour la première question. Avec une aide je trouve I1=I2=0.25A
Puis je trouve
Le point A se trouve dans l'angle supérieur à gauche.
Le point B se trouve dans l'angle inférieur à droite.
Le point C se trouve dans l'angle supérieur à droite.
Merci d'avance pour votre aide.
*** message déplacé ***
Excusez-moi pour le multi-post. Ça ne se reproduira plus. Mais alors comment dois-je faire alors pour trouver solution à mon exercice?
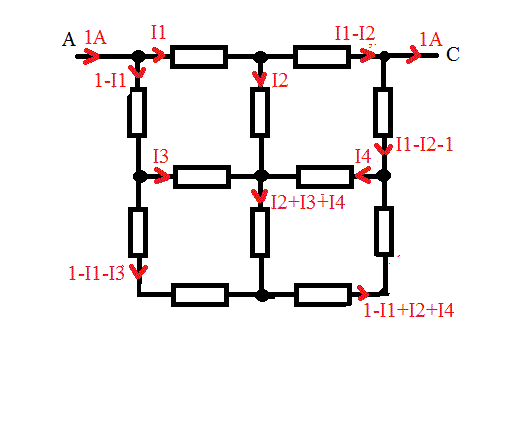
On injecte 1 A en A et ...
Equation de 5 mailles :
U(AC) = R.I1 + R(I1-I2)
U(AC) = R(1-I1) + R.I3 - R.I4 - R(I1-I2-1)
2R(1-I1-I3) - R(I2+I3+I4) - R.I3 = 0
2R(1-I1+I2+I4) + R.I4 + R(I2+I3+I4) = 0
R.I1 + R.I2 - R.I3 - R(1-I1) = 0
I1 + (I1-I2) = (1-I1) + I3 - I4 - (I1-I2-1)
2(1-I1-I3) - (I2+I3+I4) - I3 = 0
2(1-I1+I2+I4) + I4 + (I2+I3+I4) = 0
I1 + I2 - I3 - (1-I1) = 0
4I1 -2I2 - I3+I4= 2
-2I1-I2-4I3-I4 = -2
-2I1+3I2+I3+4I4= -2
2I1 +I2-I3= 1
Système qui résolu donne :
i1 = 0,625 A
i2 = 0 A
i3 = 0,25 A
i4 = -0,25 A
U(AC) = R * (0,625 + 0,625 - 0) = 0,13.R
Req = 0,13.R
-----
Rien de vérifié. 



 ) :
) :

