Inscription / Connexion Nouveau Sujet
Résistance Des Matériaux
Bonjour tout le monde, je suis bloqué au niveau de ce exercice surtout, si quelqu'un peut m'aider, merci d'avance.
voila l'énonce de l'exercice :
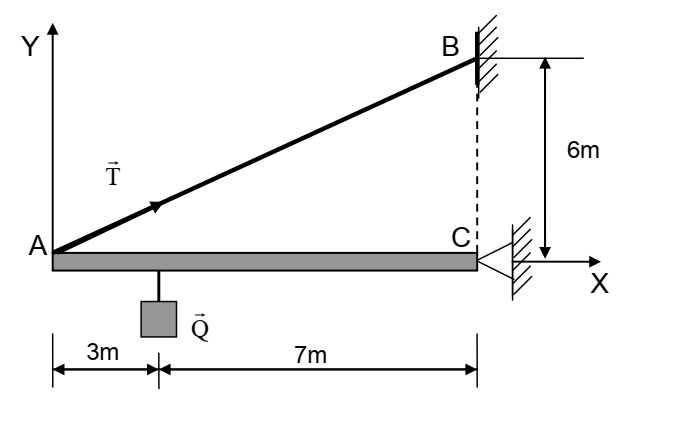
Si la charge Q se trouve à 7 m du point C, la valeur de la tension T sera égale à 15 kN.
1- Exprimer T en fonction de ses composantes Tx et Ty.
2- Donner les éléments de réduction du torseur de la tension T au point A.
3- Transporter le torseur de la tension T au point C.
Bonjour,
Je te souhaite la bienvenue sur le forum.
Pour mémoire :
Aider ne veut pas dire faire, on s'attend en effet à avoir des pistes de réflexion sur lesquelles échanger avec toi
J'attends donc tes pistes pour pouvoir démarrer,

Oui j'ai déjà fait des démarche mais c'est interdit de scanner les textes
je vais essayer de les taper
1)
AC=3+7=10
BC=6
AB2=AC2+BC2=100+36=136
AB=racine 136
On pose a l'angle entre AB et AC
Donc
sin(a)=BC/AB=6/racine 136=0,514
a=sin-1(0,514)=30,96 degre
Tx=T.cos(a)=12,86 kN
Ty=T.sin(a)=7,71kN
comment exprimer T maintenant?
1)
AC=3+7=10 unité ?
BC=6 unité ?
AB^2=AC^2+BC^2=100+36=136
AB=racine 136 unité ?
On pose a l'angle entre AB et AC
Donc
sin(a)=BC/AB=6/racine 136=0,514 le plus simple était de faire tan(a) = BC/AC = 6/10
a=sin-1(0,514)=30,96 degre ok, mais ne pas mettre autant de chiffres significatifs
Tx=T.cos(a)=12,86 kN
Ty=T.sin(a)=7,71kN
comment exprimer T maintenant?
en mathématique tu as vu comment exprimer les coordonnées d'un vecteur dans un repère, connaissant les composantes, non ?

C'est a dire
T=Tx.i +Ty.j
=12,86 k .i +7,71 k .j
???
Tu peux le mettre aussi sous la forme

C'est a dire
T=Tx.i +Ty.j
=12,86 k .i +7,71 k .j
???
Tu peux le mettre aussi sous la forme

D'accord merci
Oui c'est ça !
Pour écrire des formules mathématiques plus proprement tu devrais utiliser les outils mis à disposition par le site (clique sur le raccourci) :
 extrait de
extrait de Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
Les boutons pour éditer du Latex et l'assistant associés sont ici :

Il ne reste donc plus que la question 3.

Oui c'est ça !
Pour écrire des formules mathématiques plus proprement tu devrais utiliser les outils mis à disposition par le site (clique sur le raccourci) :
[faq]symboles[/faq]
Les boutons pour éditer du Latex et l'assistant associés sont ici :

Je sais pas comment les utiliser
Il ne reste donc plus que la question 3.

En complément (car cela va servir) : il ne faut pas oublier qu'on peut avoir une composante suivant l'axe (Oz).

En complément (car cela va servir) : il ne faut pas oublier qu'on peut avoir une composante suivant l'axe (Oz).

Mais la question 1 demande que Tx et Ty
donc on va travailer sauf avec Ox et Oy
??
En complément (car cela va servir) : il ne faut pas oublier qu'on peut avoir une composante suivant l'axe (Oz).

Mais la question 1 demande que Tx et Ty
donc on va travailer sauf avec Ox et Oy
??
En réalité, tu as trois axes à ton repère, avec une composante
Raison pour laquelle on peut ramener à un problème plan. Mais ce ne sera pas le cas du moment de la force qui sera suivant l'axe (Oz)

Si tu fais le produit vectoriel que tu as suggéré, tu dois trouver un moment

Dans les composantes de T c'est 12,86.10 puissance 3 et 7,71.10 puissance 3
n'est ce pas?
C'est difficile de te suivre comme tu n'utilises pas de symboles mathématiques ...
On retrouve bien que j'ai écrit plus haut avec la composante en kN.m
soit en N.m :
***Message corrigé***
Si tu fais le produit vectoriel que tu as suggéré, tu dois trouver un moment
J'avais effectivement oublié de préciser l'unité.

Avec plaisir !
Je te laisse réfléchir à l'autre exercice et j'y jetterai un coup d'oeil ce soir si un autre aidant ne le fait pas avant moi.
Prends le temps de t'approprier les fonctionnalités du site rappelées ci-dessus pour écrire des intégrales, des vecteurs et des produits vectoriels car ça va être illisible sinon.
Bon après-midi, 

 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum

