Bonjour,

Pourrais-tu faire un schéma clair de la situation pour être sûr que je ne réponde pas à côté ?

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Bonjour ,

ci-joint l'image correspondant .

merci de votre aide

As-tu commencé à écrire les torseurs de cohésion entre A et B et B et C ?

Ah oui désolé :

alors entre A et B j'ai les résultats suivants:

RA: 9p1l/40 , RB:11p1l/40 et MA :-7p1l^2/120

je dois poursuivre entre B et C

e tde B à C :
réaction en B : 2P2l1^2

Un schéma pour mieux fixer les idées (j'aime bien l'approche géométrique) :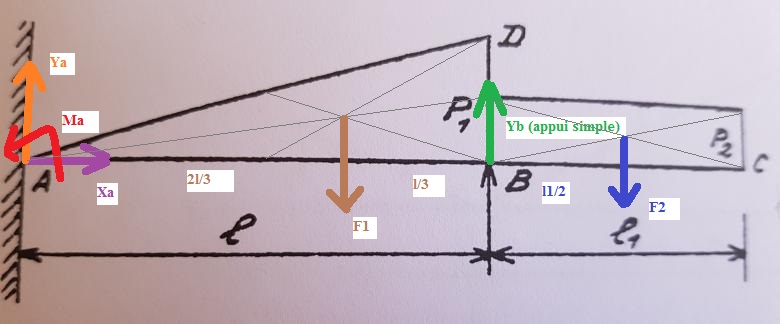



Equation de la résultant statique / (Ax) - axe horizontal :



Equation de la résultante statique / (Ay) - axe vertical :



Equation de moment en A / (Az) :



avec

et

Equation de moment en B / (Az) :



3 équations, 3 inconnues => système à résoudre



***Message complété***

Remarque importante : tu ne m'as rien précisé sur les charges uniformément réparties => à clarifier

Sur les charges réparties ? comment ça ?

donc à partir de ce que vous avez mis je fais une résolution de l'équation avec trois inconnues c'est ca

Ce que je voulais écrire : as-tu des informations sur la charge triangulaire répartie entre A et B et la charge uniformément répartie entre B et C ?

C'est en effet nécessaire pour résoudre le système de 3 équations à 3 inconnues proposé.

Ah , en gros je vais donenr l'odre de ce qui est demandé :

1) de déterminer les réactions d'appui en A ( moment d'encastrement et réaction verticale) et en B
2) de calculer la flèche de la poutre à l'extrémité de C.
3) de calculer P2 en fonction de P1, qui est donné , pour que e déplacement de l'extrémité C, sous l'action des charges appliquées soit nul .
4) faisant L=10m , L1=2,50m , P1=2000 daN , calculer Pé et tracer les diagrammes des moments fléchissants et des efforts tranchants .

Ok et donc ? Où es-tu ?

en gros j'ai répondu à la première question .
avec en réaction d'appuie en A et B
RA: 9p1l/40 , RB:11p1l/40 et MA :-7p1l^2/120
ET entre B et C :
réaction en B : 2P2l1^2

Il y a un problème dans tes calculs, tu dois forcément retrouver la même valeur pour Rb ...

As-tu vérifié qu'en remplaçant chaque terme par sa valeur trouvée dans chaque équation, tu trouvais bien une expression nulle ?

désolée je suis sur deux sujets en même temps et j'avoue que je nage dans cette matière 14 ans sans remettre le nez dedans c'est dur . en gros les premières réactions d'appuis sont celles données je sais pas pourquoi j'ai donnée une autre valeur en RB .

RA=9p1l/40 et RB=11p1l/40 et on vérifie par RA+RB =P1l /2

Je peux comprendre que tu es sur deux sujets en même temps, dis-toi que sur le forum on jongle entre plusieurs sujets en même temps (surtout en phase de confinement), donc plus du détailles les calculs effectués plus ça nous facilite la vie pour aider davantage de membres.

Pourrais-tu détailler ta méthode de résolution du système d'équation que j'ai proposé ?

De manière à identifier où il y a une erreur.

Cette détermination des efforts aux appuis par le principe fondamental de la statique est primordial pour ensuite définir les torseurs de cohésion à chaque portion de la poutre.

Merci pour la comprehension.

en gros tu as transformer les charges réparties en ponctuelles ce qui donne pour la charge triangulaire : P1*2l/3 et charge uniformement repartie : P2*L1/2

soit une équation du moment en A:

RB*l -P1*2l/3 *L/2 - P2*L1*(l/2+L1) =0

c'est ca ?

Exactement, pour cette première étape, il est plus facile de transformer les charges réparties en une force équivalente : F1 et F2.

De cette façon, on peut ensuite appliquer le PFS plus aisément.

En revanche, lorsqu'on cherchera les torseurs de cohésion, ça ne sera plus possible de considérer F1 et F2 ...

du coup si je fait le PFS j'obtient :

en A
XA=0
YA+YB-P1*2L/3-P2*L1=0
M(A): YB*l -P1*2l/3 *L/2 - P2*L1*(L+L1/2) =0

donc de la je peut en déduire YB: (P1L^2/6+ P21,5L1L)/L =0

c'est correct ? aprés je ne cache pas dans la simplification de la résolution j'ai du mal quand on divise par L c'est multiplier par son inverse c'est ca est du coup L se retrouve en bas . j'ai du mal un peu avec ca .

Attention,

En A tu un moment (liaison encastrement) à considérer.

Ce qui te fait deux équations et 3 inconnues : Ya, Yb et Ma.

Il faut donc une troisième équation pour résoudre le système.

D'où ma proposition du 24-03-20 à 12:55.

Attention, les forces équivalentes F1 et F2 que j'ai dessinées ne sont pas égales à P1 et P2, il faut penser aux formules de l'aire d'un triangle et l'aire d'un rectangle.

oui ,

du coup on aura

YA-F1+YB-F2=0
MA-2L/3*F1 +Y*BL-((L+(L-1)/2))F2=0
MA-Y*AL +F1(L/3)-(L1/2)F2=0

à partir de ces trois équations je résoue le système de trois équations 3 inconnues, c'est cela ?

Sauf erreur de ma part, nous avons déjà établi le système de 3 équations à résoudre dans mon message du 24-03-20 à 12:55.

Il faut désormais le résoudre en définissant les valeurs de F1 et F2

oui tout à fait et justement je n'arrive pas à le résoudre des difficultés à remplacer un des membres par l'équation pour tomber que sur 1 inconnu

je ne veux pas que l'on me résoue le problème mais je cherche à comprendre c'est trés important pour moi résoudre le problème ne m'aide pas a avancer mais me l'expliquer oui merci

Sauf inattention, on a le système suivant à résoudre :

(équation 1)

(équation 2)

(équation 3)

Les inconnues sont Ma, Ya et Yb, on verra plus tard pour F1 et F2

Il faut utiliser la méthode de résolution du pivot de Gauss :

* avec l'équation (1), on peut exprimer par exemple Ya en fonction de Yb, F1 et F2 :

(équation 4)

Pour supprimer Ma, fait la différence entre les équations (2) et (3)

=> tu obtiens une équation qui ne dépend que de Ya et Yb

puis dans cette équation "(2) - (3)", tu injectes la valeur trouvée avec (4) pour Ya

=> cela te permet de trouver Yb

puis ensuite tu peux en déduire Ya avec (1)

et enfin Ma avec (2) ou (3)

Donc :

Ma=LYA-L/3*F1+L1/2*F2

équation (3)+(2)
LYA -L/3*F1 + L1/2*F2- 2L/3*F1 +LYB - (L+ L-1/2)*F2=0

cela donne:

LYA +F1*(-L/3 - 2L/3) + LYB + F2 *(L1/2-(L+L-1/2))=0

si je remplace YA par l'équation (4)

F1*(1L-L/3-2L/3) + F2*(1L+ L1/2- L+L-1/2)+ YBL -YBL=0

c'est bien cela ?

Va au bout de ta logique et trouve-moi Ya, Yb et Ma.

Dans tous les cas, tu auras moyen de vérifier tes résultats en injectant les valeurs trouvées dans les équations, si à chaque fois tu trouves que c'est égal à 0, tout est bon

YB=F1L/2L - F2L1/4L - F2L/4 + F2/4

YA=F1 - F1L/2L - F2L1/4L - F2L/4 + F2/4 +F2

MA=( F1 -F1L/2L - F2L1/4L - F2L/4 + F2/4 + F2)*L -L/3 *F1+F2*L1/2

Je te fais confiance pour ces expression, j'imagine que tu as vérifié cela avec la méthode proposée ci-dessus.

Déjà tu as moyen de simplifier ces expression, n'oublie pas qu'en calcul littéral il faut simplifier autant que nécessaire.

Il reste donc enfin à déterminer la valeur de F1 et celle de F2 en fonction de P1 et P2.

Je t'ai expliqué comment faire, une idée ?

en simplifié :

YB=F1L/2L - F2*(L1/4L - L/4 + 1/4)

YA= F1*(1 - L/2L) + F2*( L1/4L -L/4 +1,25)

MA= F1* (2L/3 -L^2/2L -L1L/4L) + F2* (-L1L/4L - L^2/4 -1 + L + L1/2)

après pour trouver F1 et F2 je fais pareil que précédement je remplace F2 dans l'équation 3 ce qui me donne :

F2=YA + YB -F1

équation 3 donne alors :

MA -L*YA + L/3*F1 - L1/2* (YA + YB -F1)

F1= (MA -LYA - L1/2*YA + YB *L1/2) /( L/3 - L1/2)

et F2 = YA + YB - (MA - LYA -L1/2*YA + YB*L1/2)/(L/3-L1/2)

On commence à y voir plus clair !

Sauf la deuxième partie du raisonnement pour F1 et F2

Pour rappel :

F1 correspond à l'effort équivalent de la charge triangulaire répartie sur AB, donc

(aire d'un triangle)

F2 correspond à l'effort équivalent de la charge uniformément répartie sur BC, donc

(aire d'un rectangle)

Tu dois donc aboutir à des expressions pour Ya, Ma et Yb en fonction des notations de l'énoncé : P1, P2, l et l1

YB=P1L^2/4L - P2L1^2/4L - P2L1L/4 - P2L1/4

YA=P1L/2 - P1L^2/4L + P2L1^2/4L - P2L1L/4 +1,25P2L1

MA=P12L^2/6 -P1L^3/4L - P1L^2L1/6L - P2L1^2L/4L - P2L1L^2/4 -P2^2L1^2L/2

Essaie d'arranger un peu ces expressions car ça risque de devenir infernal pour la suite

le soucis c'est que sur l'étape de simplification j'ai du mal aprés j'arrive avec des L1^2 , des 4L avec 4 et je sais pas trop comment simplifier mieu

Je peux le concevoir en effet ...

Ton énoncé ne fournit pas des valeurs numériques ?

l'énoncé de l'exercice c'est celui ci :

1) de déterminer les réactions d'appui en A ( moment d'encastrement et réaction verticale) et en B
2) de calculer la flèche de la poutre à l'extrémité de C.
3) de calculer P2 en fonction de P1, qui est donné , pour que e déplacement de l'extrémité C, sous l'action des charges appliquées soit nul .
4) faisant L=10m , L1=2,50m , P1=2000 daN , calculer Pé et tracer les diagrammes des moments fléchissants et des efforts tranchants .

et je dois justement répondre à cela mais en question 4 , avant je dois déterminer les réactions d'appuis en A et B , calculer la fléche au point C et détermine rP2 et P1 pour ensuite faire la relation numérique

OK, pas de bol ...

On a donc vu ensemble la méthode pour la question 1.

Il faut désormais déterminer la flèche de la poutre : comment procéder ?

euh bonne question , c'est justement ma question de base lol , je ne sais par ou procéder pour obtenir la fleche .

Maintenant que tu as déterminé les efforts et moment aux liaisons (encastrement et appui), il va falloir déterminer le torseur de cohésion sur deux tronçons :

x [AB] et x [BC]

Pour ce faire, il faut constater que ce torseur se simplifie en deux composantes :
- l'effort tranchant suivant y (axe vertical) : Ty
- le moment fléchissant suivant z : Mfz.

Une fois que tu auras déterminé ces composantes sur les deux tronçons (je te préviens, ça ne va pas être une masse à faire avec ton énoncé ...), tu iras regarder dans ton cours pour avoir une expression de la dérivée du second ordre du déplacement de la poutre, en fonction de Mfz ...

Je te laisse réfléchir ...

désolée mais pour être honnête je ne vois pas ou tu veux me mener ni ou je dois m'orienter .

Tu as fait un cours de RDM ? Je commence à avoir de sérieux doutes.

Je ne peux pas faire de miracles si tu ne sais pas ce qu'est un torseur de cohésion et ses composantes : effort tranchant, moment fléchissant, ...

Sans cela, impossible de déterminer un déplacement de poutre, puis une flèche ...

en gros j'ai quittée l'école il y a 14 ans et aujourd'hui enfin y a trois ans j'ai décider de reprendre des études pour évoluer , et mon cours en statique et très léger c'est pour cela que je demande de l'aide car entre ce que j'ai appris y a trés longtemps et ce que je sais aujourd'hui et le cours je n'avance pas , maintenant je demande juste une aide , une explication pour que je comprenne

OK, je te propose de lire attentivement ce sujet que je traite en parallèle du tien pour avoir la méthode détermination d'un torseur de cohésion, bon nombre de notions du cours sont rappelées : RDM - Flexion

L'idée est de faire la même chose ici, sachant qu'il n'y aura également un effort tranchant suivant y (Ty) et un moment fléchissant suivant z (Mfz) à déterminer.

Bonjour ,

désolé pour ce retour si tardif , mais je pense avoir trouver mais pas sur on est d'accord que les torseurs de cohésion sont des PFS mais séparant les actions alors j'ai trouvais ceci:

entre A et B :

N(X)=XA
TY=-YA -PL1/2= P/3-P1L/2
MF=YAx -P1L^2/4=PX/3 -P1L^2/4

entre B et C

N(X)=0
TY= -YB-PX =-P/2 +Px
MF=YBx -Px^2/2= Px/2-PX^2/2

c'est cela ?

aprés mure reflexion est ce que on prend en compte la réaction en B dans le premier troncon ou pas du tout ?

merci de votre aide

Bonjour,

Je te réponds en fin de journée.

Il faut que je reprenne ton pb à tête reposée

Bon ...

Après m'être penché plus en détail sur ton sujet et avoir pris le temps de regarder tes propositions, je suis au regret de t'annoncer que tout ce qu'on a fait pour le calcul des appuis ne peut pas aboutir en l'état ...

Une raison initiale (que je n'avais pas vérifiée, jonglant entre les sujets sur lesquels j'interviens) : le degré d'hyperstatisme de ta poutre ...

4 inconnues, 3 équations, il est fort à parier que ton degré d'hyperstatisme est h = 1 et donc qu'il est impossible de résoudre cet exercice en faisant appel à la méthode usuelle que je t'avais proposée.

Il existe différentes méthodes, pas forcément évidentes, qui permettent de résoudre ce type de problème, par exemple la méthode des forces.

Mais ne sachant pas ce que tu as vu à l'heure actuelle, difficile d'aller plus loin en l'état ...

écouter je vais être honnête il me faut juste la fleche apres pour le reste je me débrouillerais , aprés pour calcul de la fleche ne faut t'il pas passer par la déformation de bresse ?

Comme je te l'ai écrit, là on s'est fourvoyé depuis le début c'est sur le degré hyperstatique.

Dans le cas d'un système hyperstatique, il y a deux méthodes envisageables à mon sens :
- Théorème de Ménabréa ;
- Méthode des forces

Je ne suis pas convaincu qu'on n'y arrive malheureusement avec la formule de Bresse

merci quand même de votre aide je vais essayer de trouver par un autre moyen , merci encore à vous pour votre temps