Inscription / Connexion Nouveau Sujet
réseau blazé
Bonjour,
On étudie ici un réseau blazé du schéma ci joint.
Notre étude nous a déja conduit à trouver
?Pour une seule facette (figure 2)
l'intensité diffractée et les maximum de diffraction
? Pour le réseau (figure 3)
La position des maximas principaux (ordres du réseau)
On doit maintenant estimer
- L'écart angulaire entre 2 odrdes du réseau
- La largeur angulaire de la tache de diffraction
Je pensais, pour la largeur de la tache de diffraction, faire la différence d'angle telle que
s'annule .
Quand à la différence angulaire entre les ordres, juste faire ?
C'est un peu flou pour moi 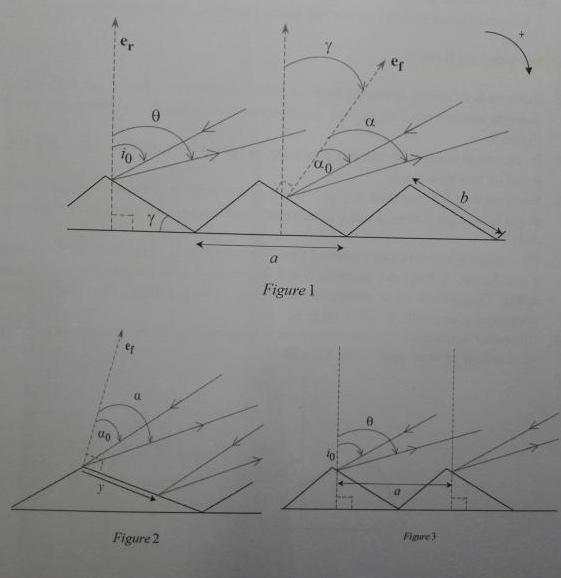
Merci d'avance pour votre aide 
bonne soirée
Bonjour,
merci pour votre réponse !
On avait pour la diffraction par une facette
En utilisant la formule fondamentale du réseau, on a eu pour les ordres du réseau.
J'ai donc fait :
largeur angulaire de la tache : On cherche le premier à gauche et à droite telle que I(
 ) s'annulle .
) s'annulle .
On obtient une largeur angulaire de
écart angulaire entre 2 ordres :
Je trouve ces résultats un peu bizarres ...
Merci encore pour votre aide 
Ces résultats ne sont pas si bizarres que çà : ils sont un peu compliqués. Dans l'énoncé, il n'y aurait pas des valeurs de a et b (disons >10  ) qui permettraient d'alléger.
) qui permettraient d'alléger.
Pour la première en rectifiant (voir le lien de vanoise) : un pb de confusion entre i0 et  0, et le classique problème de signe en réflexion (cf. votre formule du réseau)
0, et le classique problème de signe en réflexion (cf. votre formule du réseau) , soit
. En particulier, avec ce signe, on retrouve bien les lois de la réflexion.
Pour la deuxième
Si vous n'avez d'hypothèses simplificatrices (qui sont en plus raisonnables), c'est très lourd.
Bonsoir,
merci pour ces explications
je comprends mon erreur 
J'ai donc pour la largeur angulaire de la tache de diffraction
(AN :  = 0.5µm, a=0.52µm :
= 0.5µm, a=0.52µm : 
 = 0.8°)
= 0.8°)
et pour la largeur angulaire entre 2 modes : (AN :

 ' = 1.15°
' = 1.15°
Il y a donc un seul ordre dans la tache de diffraction
Cela semble t il correct ?
Merci encore 
Bonne soirée
Il y a deux problèmes dans ta réponse :
- j'ai indiqué qu'on pouvait simplifier SI "a >10  , or ici a est de l'ordre de
, or ici a est de l'ordre de  .
.
- les développements utilisés supposent que les angles soit en radian (sin(x) x en radian.)
x en radian.)
Cela semble t il correct ?
S'il s'agit de "Il y a donc un seul ordre dans la tache de diffraction", oui il y a de fortes chances, mais les calculs sont à revoir.
Tu confirmes a
 ?
?
Bonsoir,
oui nous avons a
 (nous sommes donc a la limite de l'optique ondulatoire, proche de devoir adopter un point de vue d'optique quantique ?)
(nous sommes donc a la limite de l'optique ondulatoire, proche de devoir adopter un point de vue d'optique quantique ?)
Il faut donc , si on ne veut pas faire d'approximation, utiliser et chercher la première annulation à droite et à gauche du réseau :
soit à droite
soit à gauche
et en faisant cela ne fonctionne pas par erreur de domaine (b=0.45µm <
 =0.5µm)
=0.5µm)
Il faut donc différencier l'expression  = +/-
= +/-  ? et isoler
? et isoler 
 ?
?
Merci d'avance pour votre aide 
Bonne soirée
Avant d'aller plus loin, peux-tu repréciser les données :  ,a , b,
,a , b,  , i0.
, i0.
Parce qu'on se trouve un peu aux limites
- L'écart angulaire entre 2 ordres du réseau, s'il y en a au maxi 3, voire 2 y compris l'ordre 0
- Huyghens-Fresnel idem.
•  = 0.5µm
= 0.5µm
• a calculé tel que la maximum de diffraction corresponde au premier ordre du réseau : a = 0.52µm
• b = a cos( = = 0.45µm
= = 0.45µm
• i0 = 45°
•  = 30°
= 30°
Je me suis dit que je n'allais pas intervenir mais je viens de relire l'énoncé... Après l'étude de l'intensité diffractée par une facette dont l'expression a été fournie, il s'agit bien d'étudier le réseau, c'est à dire un ensemble de N facettes ?
Bonjour,
En effet, cependant le Nombre de facette n'est donné que dans la partie suivante, on ne doit pas le faire intervenir dans cette partie
Mon raisonement pour la largeur de la tache de diffraction était de dire
soit en différenciant
mais on retrouve du  que l'on cherche, on ne peut conclure :/
que l'on cherche, on ne peut conclure :/
En effet, cependant le Nombre de facette n'est donné que dans la partie suivante, on ne doit pas le faire intervenir dans cette partie
L'énoncé , tel que tu l'as copié, précise :
Pour le réseau (figure 3)
La figure 3 correspond au cas N=2...
Je pense que l'énoncé n'est pas très clair
je pense qu'on étudie un réseau de N facettes (inconu) (figure 1)
et que la figure 2 nous permet juste d'évaluer la différence de marche entre 2 facettes successives
La largeur angulaire de la tache de diffraction ou l'écart entre 2 ordres dépend de N et on ne peut sans sortir sans l'avoir ?
je bloque à cette question
merci d'avance 
Si on raisonne numériquement ordre 1, i=15°, ordre 0 i=-45°, et il n'y a pas d'autres ordres, ou il y a qqch qui m'échappe. Et "l'écart angulaire entre 2 ordres" est de 60°.
Pour ce qui est de la largeur "à droite" de la tache, je trouve 58-(-15)=74° ! et "à gauche" pas de solution.
Soit il y a un problème dans les données, soit je suis à côté de la plaque.
Sinon, oui on étudie bien un réseau blazé.
Remarque : il faut oublier la différenciation, les variations angulaires ne sont pas faibles.
"La largeur angulaire de la tache de diffraction dépend de N."
Non elle ne dépend que de b.
"L'écart entre 2 ordres dépend de N"
Non, le passage de 2 fentes à N fentes ne change pas la position des maxi (donc des ordres), mais la répartition d'intensité, la finesse du maxi.
Est ce qu'il est possible d'avoir le sujet entier (soit un pdf, soit un lien) pour comprendre selon l'adage "pour résoudre la question N, il peut être utile de lire la question N+1".
Bonjour,
C'est la dernière question de la partie B diffraction par le réseau) ensuite nous avons une partie C (utilisation du réseau blazé pour une cavité laser) en photo
** image supprimée => ton énoncé ne semble pas faire plus d'une page, il doit donc être recopié **
Bonjour,
J'ai été fouillé du côté "grating external cavity laser".
J'ai trouvé en effet des réseaux blazés avec des pas jusqu'à 100 nm, donc pas de problème de valeur numérique, et donc des nombre d'ordre très limités comme ici.
Par contre, je n'ai trouvé que des calculs d'ordre, pas de calcul de diffraction : la formule d'Huygens-Fresnel à de telles largeurs et de tels angles est très limite.
Pour la question 9), en supposant malgré tout que cela soit correct, il y a uniquement deux ordres, l'ordre 1 coïncidant avec le maxi de diffraction et l'ordre 0 avec une intensité de 20% de celle de l'ordre 1.
Bonsoir,
un petit retour sur cette question qui nous avait posé quelques tracas :
Nous avons corrigé l'exercice
Pour la largeur de la tache de diffraction, le raisonnement proposé était le bon, les valeurs i0 et  avaient été mal définies dans le sujet, d'où l'absence de solution gauche
avaient été mal définies dans le sujet, d'où l'absence de solution gauche
Merci pour votre aide précieuse 
Bonne soirée


