Hello!
Ton énoncé n'est pas très clair! Un peu plus d'informations sur l'exercice s'il te plait.
Mais ta première idée est bonne!

Mais tu as dis un truc qui n'est pas bon. Tu ne peux pas considerer que la vitesse de A est nulle dans R₀ car tu ne connaît pas la nature exacte du mouvement. Par contre, elle est nulle dans S

Bonjour,
le système étudié est composé par le solide (S) qui est  une plaque triangulaire équilatérale ABC de masse m,de coté a et d'épaisseur négligeable et d'une tige (T) infuniment mince de longueur b et de masse négligeable.
Le repère S=(A,x,y,z) est lié à (S) tel que (A,y)soit parallèle à BC.
La tige(T) est soudée à  (S) au point A de telle sorte que la liaison en A est telle que le plan de (S) reste vertical et constamment perpendiculaire à (T) au cours du mouvement.(T)est confondue avec l'axe (O,x).Le résultat doit être exprimé dans le repère S=(A,x,y,z)

J'hésite avec l'expression de la vitesse de A dans Ro:Si j'exprime OA dans le repère S,alors est ce que le vecteur OA sera ?donc la vitesse de A sera
Cordialement

Bonjour,
Voici le schéma lié au problème:



** image supprimée **

Bonjour
Comme te l'a fait remarquer  bissinyandoup, ta façon de t'exprimer dans tes premiers messages n'est pas claire. Il s'agit, me semble-t-il, d'exprimer la vitesse de A dans Ro en fonction des vecteurs unitaires de la base locale , comme il est fréquent, lors de l'étude du mouvement circulaire, d'exprimer la vitesse et l'accélération absolues en fonction des vecteurs unitaire de la base polaire locale .
D'accord avec l'expression de la vitesse de A que tu fournis dans ton dernier message.

Bonjour,
Est-ce que l'expression de la vitesse de A dans le message précedent est toujours valide même si A n'est pas confondu avec O? En écrivant le vecteur OA dans Ro ,puis en dérivant par rapport au temps et enfin en réexprimant dans S, cela donne un résultat différent du message précedent:
Merci infiniment

L'angle n'intervient pas dans l'étude du mouvement de A mais il s'agit peut-être de ta part d'une étourderie de saisie de formule. La méthode  alternative que tu proposes est tout à fait cohérente avec le résultat précédent.


Je dérive par rapport au temps dans Ro :


Or, justement :


J'ai noté "psi point" : ( ) la dérivée de par rapport au temps.

Merci beaucoup!

Bonjour,
J'ai encore une question:
Ici la plaque peut tourner autour de l'axe (Ox) tout en restant perpendiculaire à la tige,mais alors devrait avoir une composante suivant ?
Cordialement

Ta question n'est pas très claire. Mais si je t'ai bien compris, tu penses que le fait que la plaque tourne autour de (Ox)  modifirait l'expression de y et par consequent changerait l'expression de V(A) c'est ça ?

Et bien a mon avis, Non, car si le seul mouvement de la plaque est le mouvement de rotation autour de (Ox), alors, le point A ne se déplacera pas. Et conséquent V(A/R₀) ne changera pas. (Sauf erreur)

J'a i commis une erreur en oubliant la rotation de la plaque donc en oubliant que les vecteurs unitaires et tourne à la vitesse angulaire (point) autour de la tige.
Si tu définit le vecteur unitaire appartenant au plan (O,xo,yo) et perpendiculaire à la tige. Tu as :


Le vecteur n'est égal au vecteur (y) que dans le cas particulier =0. Dans le cas général, dépend de et des vecteurs unitaires (y) et (z). Je te laisse faire le calcul.
Désolé : je n'avais pas lu attentivement l'intégralité de l'énoncé précédemment...

Bonsoir à tous
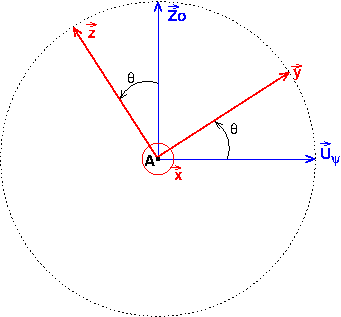
Le dessin est trompeur

Le vecteur y n'est pas normal à z_o mais à z si je lis bien
Donc effectivement V(À)/R_o ne peut pas être colinéaire à y
(Sauf pour = k)

Sauf erreur☺

Oups
Pas vu ton message Vanoise, désolé

Bonsoir krinn
Pas de problème ! Les messages croisés sont inévitables !  

Pour illustrer ce qui précède, voici un schéma avec pour plan de figure le plan (A,y,z) vertical perpendiculaire à la tige (OA), le vecteur unitaire (x) étant orienté vers l'avant de la figure.

Bonjour,
Merci beaucoup pour vos réponses,si je représente V(A)/Ro dans (S),ne s'annule telle pas puisque le repère S a pour origine A?
Cordialement

Relis bien mon message du  02-02-18 à 12:11 sauf la dernière ligne qui est fausse.
Ta phrase :

Merci encore Vanoise!Je m'excuse vraiment pour les questions...

Bonsoir,
Est-ce qu'on peut calculer la vitesse de A avec là règle de dérivation?
,
est le vecteur rotation instantanné de la tige par rapport à Ro
Je trouve
Est-ce bien la vitesse de A?
Je vous remercie

Bonjour
Mais justement : la vitesse de A dans Ro s'écrit :


Que vient faire un vecteur rotation ici ?
Si tu fais le calcul direct, tu obtiens le résultat que je t'ai fourni dans mon message du 2/2/18 à 14h01.

L'autre façon simple de faire consiste à écrire comme cela a déjà été fait :


puis de remarquer, en utilisant éventuellement le schéma que j'ai fourni dans mon message du 2/2/18 à 19h51 :


Il s'agit bien de ce que tu obtiens.

Je crois que tu confonds avec la formule du « champ de vitesse », c'est à dire la formule qui permet d'obtenir la vitesse d'un point quelconque d'un solide, connaissant la vitesse d'un point particulier de celui-ci et le vecteur rotation instantanée caractérisant le mouvement du solide.

Par exemple ici, si (S) désigne la plaque triangulaire, il est possible de définir un vecteur rotation instantanée caractérisant la rotation de (S) par rapport à Ro. La vitesse d'un point quelconque de (S), le point B par exemple, peut s'écrire :

Re,
Je crois que 'ai fait une erreur dans l'expression :je devrai écrire ,puisque A est fixe par rapport au repère de la tige,alors
Cordialement

Effectivement : il est possible de passer par la relation de composition des vitesses comme tu l'as fait dans ton message de 17h22. Tu pouvais aussi appliquer dans Ro la formule du champ de vitesse en considérant que O et A appartiennent à la tige (T), la vitesse de O dans Ro étant bien sûr le vecteur nul :

Merci beaucoup Vanoise!