Inscription / Connexion Nouveau Sujet
relation sur la thermodynamique
bonsoir besoin d'aide sur cet exercice
à une pression de 40 atm, un gaz diatomique obéit à:
En déduire l'équation d'état
Bonsoir
Commence par revoir la définition de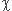 
T
Tu obtiens alors deux équations aux dérivées partielles.
Tu connais sûrement celle des gaz parfaits. Plus généralement, il s'agit de la relation existant entre P, V et T pour une quantité fixe de matière de la forme :
P=f(V,T).
La seconde relation fourni la dérivée partielle de P par rapport à T.
La première relation, moyennant une petite manipulation, permet d'obtenir la dérivée partielle de P par rapport à V.
Par intégration, on obtient P=f(V,T).
Revois ton cours de mathématiques sur ce sujet : l'inverse de la dérivée de V par rapport à P est égale à la dérivée de P par rapport à V.
Cela te conduit à la situation décrite dans mon message précédent.
La seconde relation indiquée dans l'énoncé est :
Tu peux intégrer par rapport à T en considérant V comme une constante. Cela va te donner une expression de P en fonction de V et T à une fonction de V près puisque, l'intégration s'effectuant à V constant, la « constante » d'intégration peut dépendre de V.
La première relation, après la manipulation indiquée conduit à :
En dérivant la relation précédente par rapport à V, tu vas obtenir P=f(V,T) à une constante près ; tu peux déterminer cette constante sachant que la pression tend vers zéro quand T tend vers zéro. Cela va t'amener à une variante de l'équation d'état d'un gaz.
Attention au niveau des notations à ne pas confondre le symbole « « utilisé pour les dérivées partielles avec la lettre grecque
utilisée le plus souvent pour désigner une quantité élémentaire : W par exemple.
Bonsoir
La seconde relation indiquée dans l'énoncé est :
En dérivant la relation précédente par rapport à V, tu vas obtenir P=f(V,T) à une constante près ; tu peux déterminer cette constante sachant que la pression tend vers zéro quand T tend vers zéro. Cela va t'amener à une variante de l'équation d'état d'un gaz.
vous vouliez dire en integrant je suppose?
Pour la relation 1 de l'énoncé j'ai obtenue P=
en intégrant la 2eme relation j'obtient le même résultat.
C'est bien cela. Il s'agit de l'équation d'état d'un gaz parfait auquel on ajoute le terme correctif en (a/V).
Remarque au niveau des dimensions : V désigne le volume molaire et non le volume. Sinon, il faudrait faire intervenir n, la quantité en moles.
L'intégration de la première relation de mon message du 24-02-20 à 23:21 fournit l'expression de P à une fonction près de V . Tu sais bien en math que prendre les primitives de deux expressions introduit une égalité des primitives à une constante près. Comme le premier calcul de primitive se fait à V fixe ; le calcul de primitive introduit en fait une expression de V.
La première relation conduit rigoureusement à :
La seconde relation est indispensable pour obtenir f(V). Elle conduit en dérivant l'expression précédente à :
Cela conduit à une dérivée f'(V)=O. f(V) est en fait une constante K. On obtient donc :
On obtient K=0 en remarquant que :
à bientôt 
Annuler
connectez vous