Niveau licence

Relation de conjugaison avec origine au sommet

Posté par
khalido 19-02-20 à 21:52

Bonjour

Comment je peux montrer que :

n/CA' - n'/CA = n-n'/CS

bien sûr on sait que
n'/SA' - n/SA = n'-n/SC
et
SA'= SC + CA'
SA = SC + CA

Posté par re : Relation de conjugaison avec origine au sommet 19-02-20 à 21:57

Bonsoir
Si tu admets la formule de conjugaison avec origine au sommet, tu déduis celle avec origine au centre par application de la relation de Chasles.

Posté par re : Relation de conjugaison avec origine au sommet 19-02-20 à 22:03

Quelle est la relation de Chasles ?

Posté par re : Relation de conjugaison avec origine au sommet 19-02-20 à 22:29

La relation de Chasles conduit aux deux dernières égalités que tu as écrites. En les combinant à la première relation de conjugaison, tu obtiens la seconde. Il y a un peu plus rapide et élégant en partant d'une figure et en exprimant le grandissement transversal de 2 façons différentes.

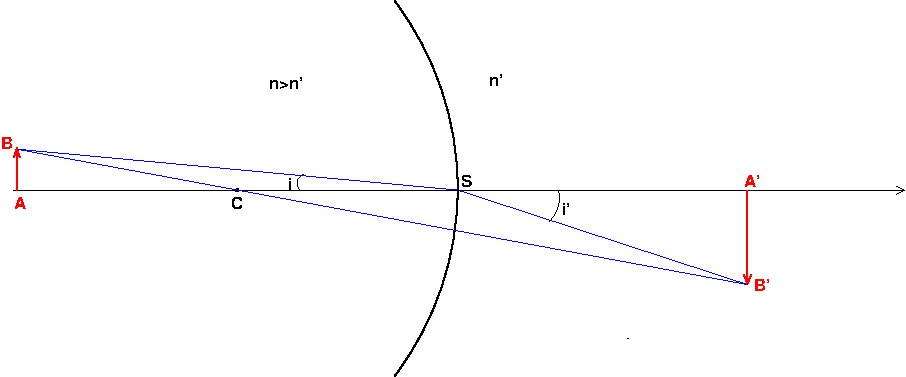
Posté par re : Relation de conjugaison avec origine au sommet 19-02-20 à 23:37

Voila une figure qui devrait t'aider. Les formules sont valides dans les conditions de Gauss ; les angles i et i' sont suffisamment petits pour pouvoir confondre au premier ordre près, le sinus et la tangente. Puisque le rayon passant par le sommet S vérifie la loi de Descartes sur la réfraction :

$\frac{n'}{n}=\frac{\sin\left(i\right)}{\sin\left(i'\right)}=\frac{\tan\left(i\right)}{\tan\left(i'\right)}=\frac{\overline{AB}}{\overline{AS}}\cdot\frac{\overline{\overline{A'S}}}{\overline{A'B'}}$

soit le grandissement transversal :

$\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{n.\overline{SA'}}{n'.\overline{SA}}$

D'autre part, le rayon passant par le centre C du dioptre sphérique n'est pas dévié :

$\frac{\overline{AB}}{\overline{AC}}=\frac{\overline{A'B'}}{\overline{A'C}}\quad soit\quad\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{CA'}}{\overline{CA}}$

En identifiant les deux expressions du grandissement, on obtient :

$n\cdot\frac{\overline{CA}}{\overline{SA}}=n'\cdot\frac{\overline{CA'}}{\overline{SA'}}$

puisque : $\overline{SA}=\overline{SC}+\overline{CA}$ et $\overline{SA'}=\overline{SC}+\overline{CA'}$ , un produit en croix conduit à la formule de conjugaison recherchée.
Je te laisse terminer...

Relation de conjugaison avec origine au sommet