Inscription / Connexion Nouveau Sujet
Régime variable
Bonjour, j'avais plutôt compris avec les régimes stationnaires mais j'ai un peu de mal avec les régimes variables, et ceci dès la première question...
Voici le sujet:
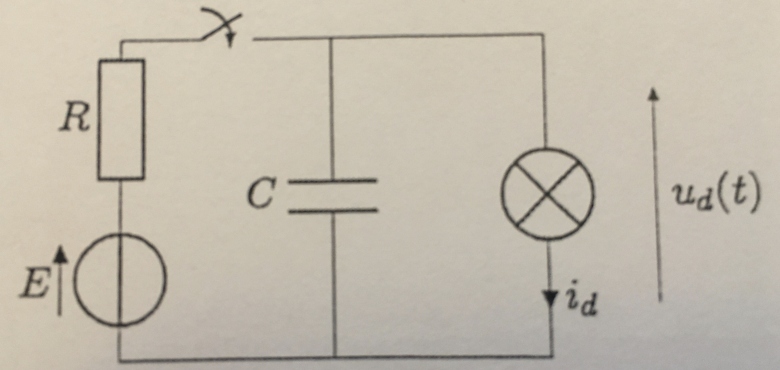
« Une lampe à décharge, dont la tension entre ses bornes est notée ud(t), possède les caractéristiques suivantes :
- Si la lampe est éteinte, elle se comporte comme une résistance infinie et reste éteinte tant que |ud(t)|<Ua. La tension Ua est la tension d'allumage.
- Si la lampe est allumée, elle se comporte comme une résistance de valeur Rdet reste allumée tant que |ud(t)|>Ue. La tension Ue est la tension d'extinction et Ue<Ua.
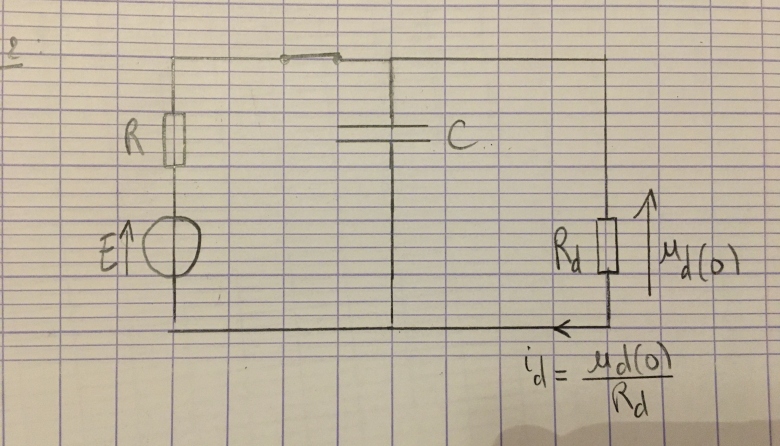
(Voir image circuit ci-dessous)
Q1. Tracer la caractéristique de l'intensité id fonction de la tension udde la lampe à décharge lors d'une phase de charge allant de ud= 0 à ud=Umax avec Umax>Ua. Tracer ensuite la même caractéristique pour une phase de décharge allant de ud=Umax à ud= 0.
Pour t<0 le condensateur est déchargé et l'interrupteur est ouvert. À t=0 on ferme ce dernier.
Q2. Quel est alors l'état de la lampe? Représenter le schéma du circuit étudié dans cette phase.
Q3. Déterminer, en utilisant le comportement en régime permanent du condensateur, la valeur finale atteinte par ud.
Q4. Établir l'équation différentielle vérifiée par ud(t). La résoudre.
Q5. Donner une condition sur la f.e.m. E pour que la lampe s'allume. Si cette condition est vérifiée, exprimer le temps d'allumage Ta.
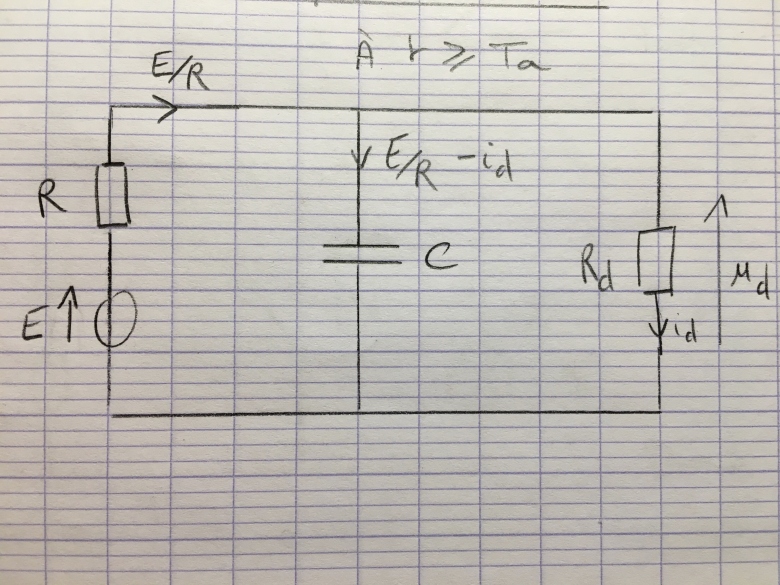
On s'intéresse maintenant à ce qu'il se passe lorsque la lampe est allumée.
Q6. Représenter le circuit dans ce cas et y introduire les grandeurs électriques nécessaires.
Q7. Déterminer, en utilisant le comportement en régime permanent du condensateur, la valeur finale atteinte par ud
Q8. Établir l'équation différentielle vérifie ud(t) pour t>Ta. La résoudre (On fera attention au fait qu'ici l'instant initial correspond à l'instant Ta.
Q9. Sous quelle condition la lampe peut-elle s'éteindre ? »
Merci pour votre aide
Kekeee
Bonjour,
Q1 n'est pas un problème de régime variable, mais de traduction d'un texte en courbe :
Il faut tracer id(ud) sachant que :
- Si la lampe est éteinte, elle se comporte comme une résistance infinie et reste éteinte tant que |ud(t)|<Ua.
- Si la lampe est allumée, elle se comporte comme une résistance de valeur R
Puis retour
- ... elle se comporte comme une résistance de valeur Rd ... tant que |ud(t)|>Ue
Bonjour gts2 merci pour votre réponse et veuillez m'excuser pour ma réponse tardive.
Ok mais je ne vois toujours pas comment le traduire en courbe... j'ai un peu de mal.
Partie 1 : elle se comporte comme une résistance infinie et reste éteinte tant que |ud(t)|<Ua.
donc : ud varie de 0 à +Ua et i vaut (résistance infinie) ?
Partie 2 : elle se comporte comme une résistance de valeur R tant que |ud(t)|>Ue
donc : ud varie de Ue à l'infini i= ?
Partie 1:
Avec une résistance infini i vaut 0
Partie 2:
I=ud/Re
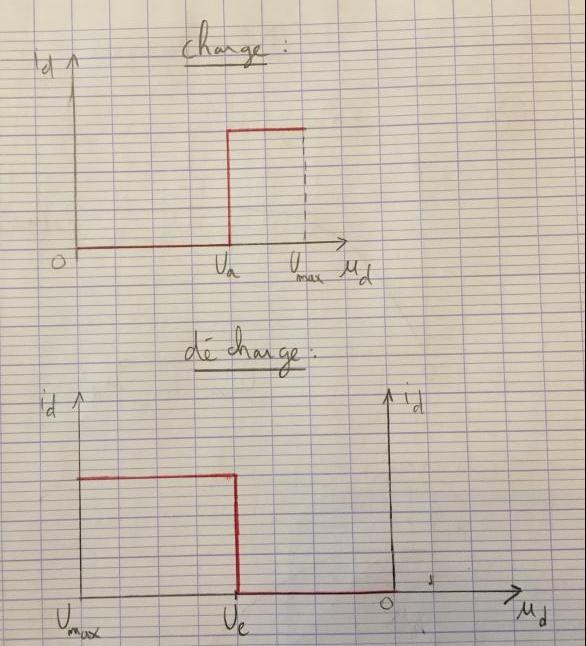
A t'on ce genre de graphique du coup?
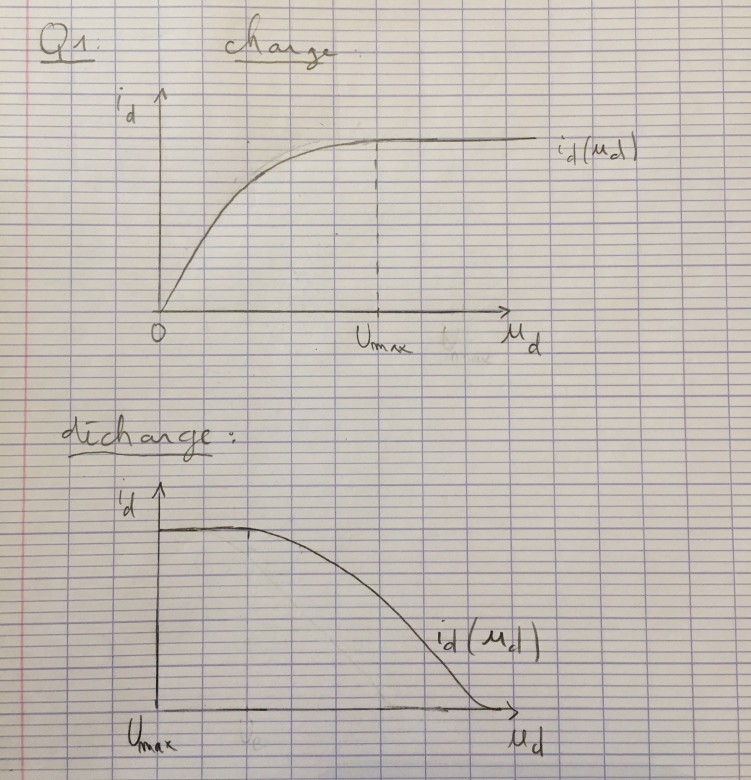
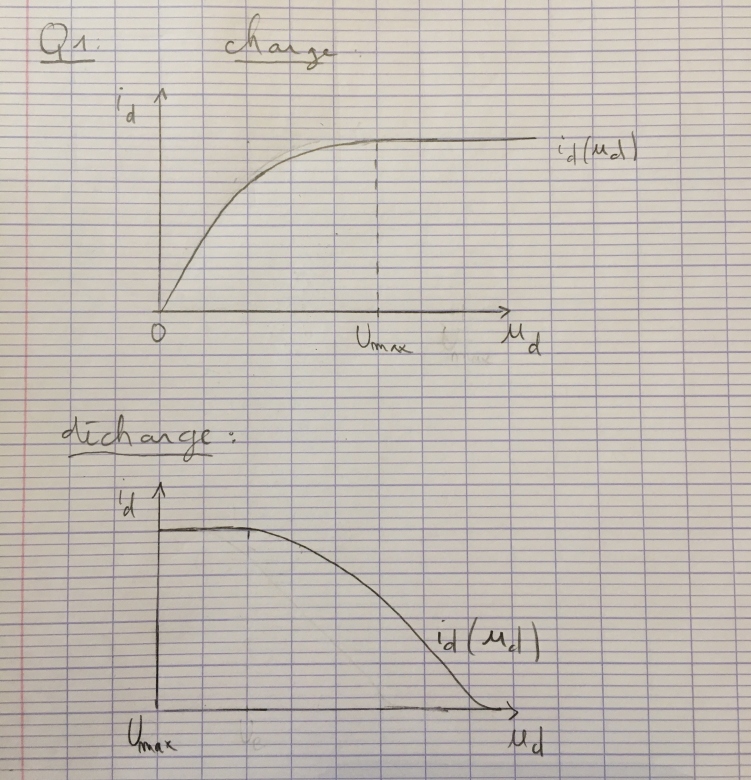
Partie 1 : Avec une résistance infini i vaut 0
C'est bien cela, mais où voyez-vous une branche i=0 sur vos graphes ?
Partie 2 : I=ud/Re
C'est bien cela, et c'est l'équation d'une droite passant par (0,0), où voyez-vous une telle droite sur vos graphes ?
De plus sur les graphes devrait apparaitre les limites Ua et Ue.
C'est mieux : on a le segment de droite id=0 de ud=0 à ud=Ua.
Il s'agit maintenant de tracer le segment de droite, id=ud/Re, de ud=Ue à ud=Umax.
Pour se simplifier la vie et en vue des questions suivantes, il vaut mieux n'avoir qu'un seul graphique.
Mais je ne comprends pas votre problème : tracer une droite (plus exactement un segment) y=ax, vous devez savoir faire cela depuis le collège.
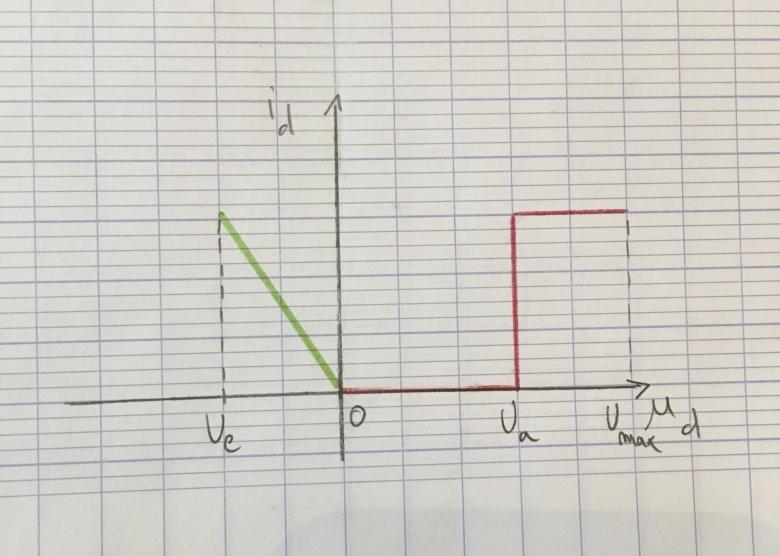
On se rapproche :
La courbe i=0 n'est vrai que de 0 à Ua, donc la branche horizontale rouge au-delà de Ua n'a pas de sens.
Ce n'est pas indiqué explicitement dans le texte, mais Ue>0
Une droite i=u/RT a une pente positive, votre droite verte a une pente négative.
Ce segment de droite doit aller de Ue à Umax
Ok mais vous m'avez dit que ma droite d'équation i=u/RT devait passer par (0,0) donc si on la trace de Ue>0 à Umax>Ue elle ne peut pas passer par (0,0) non?
Faites-le en deux fois :
- tracez une droite de pente positive passant en (0,0), c'est la traduction de i=u/R ( disons en pointillé).
- puis ne retenez que le segment de cette droite qui va de Ue à Umax, c'est la traduction de Ue est la tension d'extinction et de u maxi = Umax
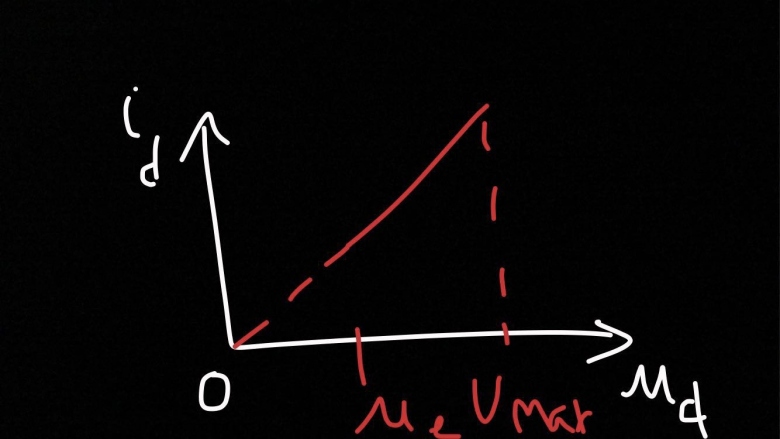
Ce coup-ci, c'est bon.
Mettez les deux sur le même graphe.
Il faut maintenant le faire fonctionner : le point de fonctionnement ne peut être que sur l'un des deux segments (éteint ou allumé).
Supposez que vous partiez de u=0 et que vous augmentiez u, vous restez sur la courbe éteinte jusqu'à u=Ua et si vous dépassez Ua, vous sautez sur la courbe allumée.
Et réciproquement quand partant de Umax, vous diminuez u.
Voici les deux courbes sur le même schéma:
Vos explications sont très claires merci, elles concernent la question 3?
Par contre je n'ai pas très bien compris ce que vous appelez point de fonctionnement?
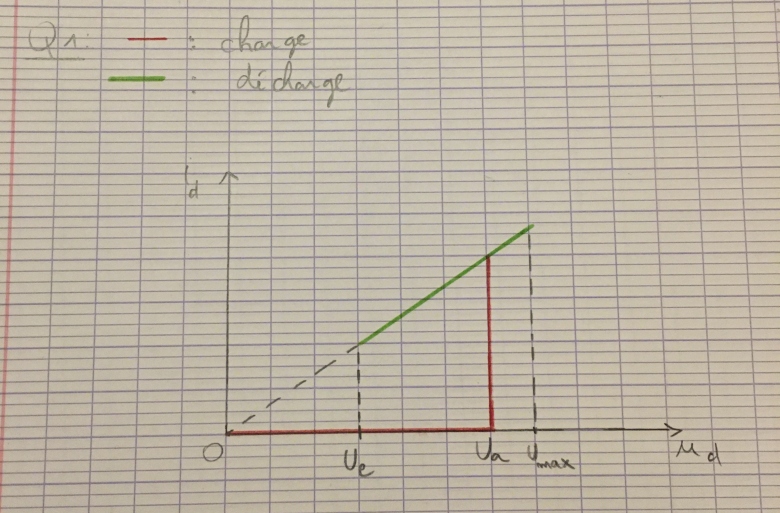
Vous avez bien compris.
Le point de fonctionnement, c'est simplement le couple (u,i) à un instant donné.
Votre graphe va servir pour Q2 et Q3, comme support de raisonnement.
C'est grâce à vos explications
Alors pour la Q2: à t=0 la lampe est allumée, et a une tension à ses bornes égale à ud(0)>Ue. (Je ne sais pas si on peut aussi dire que ud(0)>Ua).
Elle correspond ainsi à une résistance de valeur Rd.
Et voici le circuit à étudier dans cette phase
Non je me suis trompé à t=0 la lampe n'est pas allumée, mais alors je ne vois pas ce qui se passe...
C'est bien cela, la lampe n'est pas allumée, donc id=0 (ou Rlampe infinie si vous préférez), vous avez un simple circuit ERC.
Bonsoirgts2, je suis vraiment désolé, l' heure c'est un peu rallongée...
Pour Q2;
On sait que à t<0, id=0 et donc ud=0 (u=L*di/dt)
À t=0 ud est continue et ud=0 et id=ud/r =0 ( Loi d'Ohm avec la lampe qui se comporte comme une résistance infinie, i.e un interrupteur ouvert).
=0 ( Loi d'Ohm avec la lampe qui se comporte comme une résistance infinie, i.e un interrupteur ouvert).
Comme u=q/C, et ud=0 alors q=0 et le condensateur se comporte comme un file.
Je ne sais pas si mon raisonnement est juste...
(Voir schéma circuit)
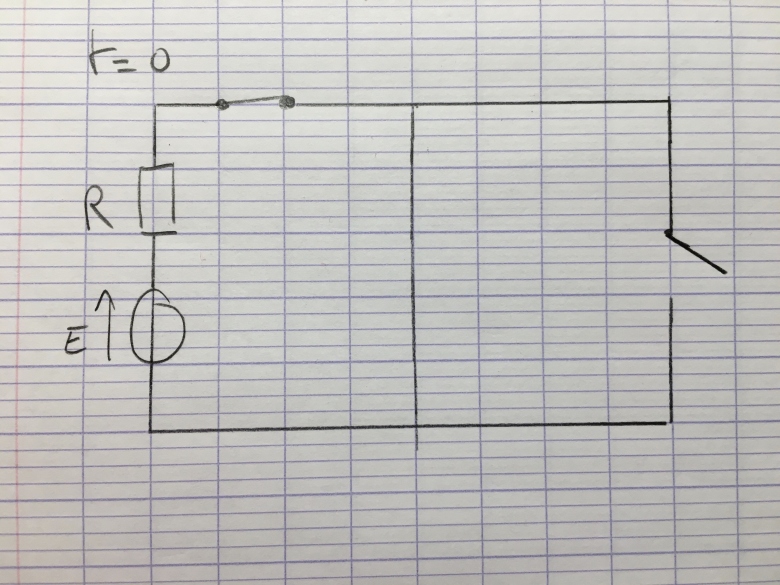
Pour la Q3:
En regime permanant continu, le condensateur est équivalent à un interrupteur ouvert et ud ne dépend pas du temps donc quand t
 , ud[sub]
, ud[sub] [/sub]=E
[/sub]=E
(Voir schéma circuit suivant):
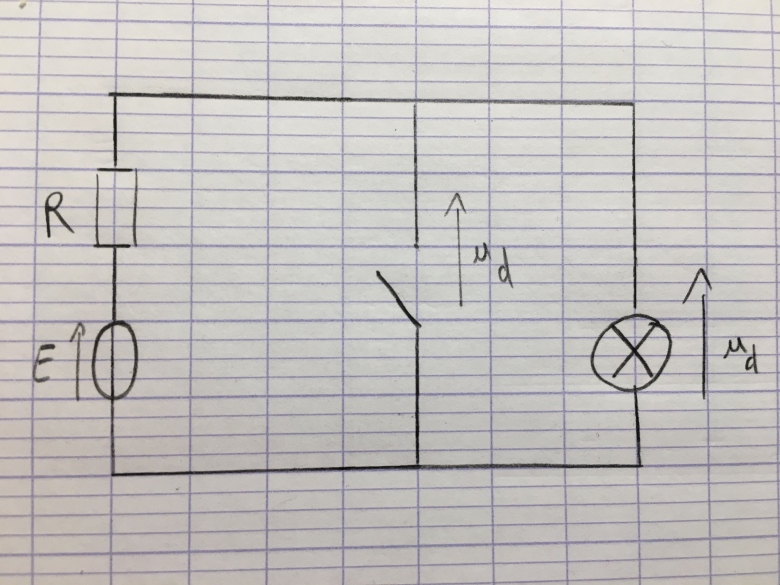
Ensuite pour Q4:
E(t)=ud(t)+Rid(t)
Donc;
E(t)=ud(t)+RCdud/dt
Soit;
dud/dt+ud/RC=E/RC
On pose  :=RC
:=RC
Alors;
dud/dt+ud/ =E
=E
•Equation homogène associée:
dud/dt+ud/ =0
=0
Donc;
ud[sub]hom[/sub](t)=Ae-t/ . A
. A
 .
.
•Solution particulière de l'équation différentielle complète:
Ici constante car le second membre est constant.
dud[sub]part[/sub]/dt+ud[sub]part[/sub]/ =E/
=E/
Solution particulière :
ud[sub]part[/sub]=E ( car la dérivé de ud[sub]part[/sub] est nulle car ud[sub]part[/sub] constant).
Ainsi; ud(t)=Ae-t/ +E
+E
ud continue en 0:
ud(0)=0=ud(0+)=A+E
Donc A=-E
Donc à t 0;
0;
ud(t)=E(1-e-t/ )
)
Voilà j'hésite aussi...
Ensuite pour Q5:
On veut que |ud(t)| Ua
Ua
Soit
|E(1-e-t/ )|
)| Ua
Ua
Soit
E|(1-e-t/ )|
)| Ua
Ua
Or pour t 0;
0;
e-t/
 1
1
D'où la condition;
E Ua/(1-e-t/
Ua/(1-e-t/ )
)
(Je crois qu'il y a un problème ici pour t=0... on divise par 0 je ne sais pas si ça se fait...)
Donc si cette condition est vérifiée, on a:
E(1-e-t/ )
) Ua
Ua
ssi E-Ee-t/
 Ua
Ua
ssi Ee-t/
 -Ua+E
-Ua+E
ssi e-t/
 1-Ua/E
1-Ua/E
ssi -t/
 ln(1-Ua/E)
ln(1-Ua/E)
ssi t -
- ln(1-Ua/E)
ln(1-Ua/E)
Donc Ta=- ln(1-Ua/E)
ln(1-Ua/E)
Ensuite pour Q7:
ud=Rd*id (loi d'Ohm)
Or quand t +
+ , le condensateur équivaut à un interrupteur ouvert.
, le condensateur équivaut à un interrupteur ouvert.
Doncid-E/R=0 i.e id=E/R
Donc ud[sub]max[/sub]=RdE/R
Pour Q8, on a:
dud/dt+ud/RC=E/RC
On pose  =RC
=RC
Alors dud/dt+ud/ =E/
=E/
•Equation homogène:.
ud hom=Ae-t/
•Solution particulière (constante):
ud part=E
ud(Ta)=Ua
Donc Ae-Ta/ +E=Ua
+E=Ua
Donc A=(Ua-E)/e-Ta/
Finalement,
ud(t)=(Ua-E)/e-Ta/ e-t/
e-t/ +E
+E
ud(t)=(Ua-E)e-t/ +Ta/
+Ta/ +E
+E
ud(t)=(Ua-E)e(Ta-t)/ +E
+E
Enfin pour Q9:
La lampe peut s'éteindre si et seulement si:
|ud(t)| Ue
Ue
| |Ua-E|e(Ta-t)/ +E |
+E | Ue
Ue
E(1-e(Ta-t)/ )
) Ue-Ua*e(Ta-t)/
Ue-Ua*e(Ta-t)/
E (Ue-Ua*e(Ta-t)/
(Ue-Ua*e(Ta-t)/ )/(1-e(Ta-t)/
)/(1-e(Ta-t)/
VOILÀ en attente de vos réponses je vous prie encore de m'excuser et d'accepter mes sincères salutations
Q2 : le condensateur est certes déchargé, mais il est là.
Q3 : la lampe est toujours éteinte, u vaut bien E
Q4 : OK
Q5 : OK pour Ta. Pour la condition sur E, elle ne doit pas dépendre de t, il est plus simple de raisonner à l'envers : la lampe reste éteinte si u<Ua qelque soit t et donc ?
Q6 : le schéma est le bon, mais pas les courants : E/R n'est vrai qu'à t=0.
Q7 : même erreur qu'en Q6, mais faites le schéma, il est tout simple
Q8 : vous reprenez l'équation Q4, or le schéma n'est pas le même, il faut donc reprendre.
Connaissez-vous Thévenin ?
Q9 : raisonnement correct, mais comme il y a un pb en Q8.
Bonjour gts2,
Q5:la lampe reste éteinte quelque soit t donc si et seulement si Rdid<Ua ou E<Ua je ne sais pas trop
Q6: Je ne comprends pas pourquoi c'est bon pour t=0 mais pas pour tout t 0?
0?
Q7: Je ne comprends pas pourquoi... désolé
Q8: Oui je connais Thevenin mais j'ai énormément de mal à m'en servir et à comprendre...
Q9: Oui forcément avec le pb question 8 je ne peux pas conclure
Q5:la lampe reste éteinte quelque soit t donc si et seulement si Rdid<Ua ou E<Ua je ne sais pas trop
Si la lampe est éteinte, il y a des chances que id=0 !
Q6: Je ne comprends pas pourquoi c'est bon pour t=0 mais pas pour tout t0
Comment avez-vous obtenu E/R ? Et idem pour Q7.
Q8: Oui je connais Thevenin mais j'ai énormément de mal à m'en servir et à comprendre...
Pourtant dans ce cas là, c'est quand même utile : avec le générateur de Thévenin, le schéma est identique à Q4 avec de nouvelles valeurs de E et R, donc une fois Thévenin effectué , c'est fini.
Je n'ai pas compris pour la question 5...
On obtient i=E/R avec la loi d'Ohm simplement non?
Pour Q7 comme le condensateur est équivalent à un interrupteur ouvert, l'intensité aux bornes du condensateur est nulle donc id=E/R...
Pour Q8 je vais essayer de refaire le schéma et je vous renvoie ce que j'ai trouvé dans peu de temps
On obtient i=E/R avec la loi d'Ohm simplement non ?
La tension aux bornes de R ne vaut E qu'à t=0.
l'intensité aux bornes du condensateur est nulle
N'a pas de sens : c'est soit la tension aux bornes (non nulle) soit le courant traversant (qui est bien nul)
id=E/R
Même remarque que précédemment, la tension aux bornes de R n'est pas E.
Voir votre schéma du 04-01-21 à 20:48
Q5 : la lampe reste éteinte si à tout instant t
Donc pour Q5, la condition pour que la lampe s'allume est juste E Ua on est d'accord?
Ua on est d'accord?
Pour Q6: Et pour t 0 que vaut la tension? E=Ri+ud(t)?
0 que vaut la tension? E=Ri+ud(t)?
Oui pardon pour Q7; le courant est nul* et E=Ur+Ud?
Q5 : OK
Q6 : E=Ri+ud(t) : OK
Q7 : E=Ur+Ud : OK, mais si on tient compte du courant nul dans la capacité, vous devriez reconnaitre un diviseur de tension.