Inscription / Connexion Nouveau Sujet
régime transitoire des cicruits RC
Bonsoir,
J'ai un dm de physique a faire mais je ne sais pas vraiment comment débuter cette éxercice.
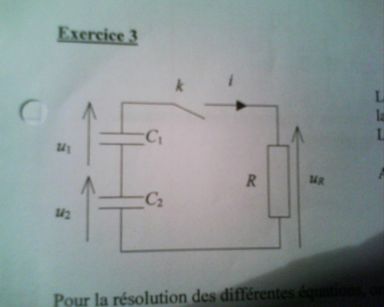
Exercice:
Le condensateur C1 est initialement chargé sous la tension Uo (positive).
Le condensateur C2 est initialement décharché.
A l'instant t=0, on ferme l'interrupteur k.
Pour la résolution des differentes équations, on posera: 1/C=1/C1+1/C2
1. Etablir l'equation différentielle du courant i(t). En déduire l'expression de i(t).
2. Montrer que la grandeur C1u1-C2u2 est constante. Exprimer cette constante en fonction de Uo.
3. Etablir l'équation différentielle de la tension u1(t). En déduire l'expression de u1(t).
4. Etablir l'équation différentielle de la tension u2(t). En déduire l'expression de u2(t).
5. Représenter sur un meme graphique les tensions u1(t) et u2(t).
6. Faire un bilan énergétique du système. Déterminer l'expression de la quantité d'énergie dissipé par effet joule pendant le régime transitoire.
Voila
j'ai commencé pour la question 1 par remplacer les deux condensateurs en serie par 1 condensateur mais avec cette histoire que un est chargé et l'autre déchargé je ne sais pas comment faire... :'(
merci d'avance !
ce que j'ai fais c'est ca: j'ai mis les deux condensateurs en 1
i= C du/dt
u=-R.i
du/dt= -R di/dt
i/C=-R di/dt
i-RC di/dt=0
i+RC di/dt=0
du type: i=Be(-t/ )
)
Condition Initial: a t=0, i(0)=B=Uo/R
i(t)=Uo/R e(-t/ )
)
pour de ce qui est de la grandeur C1u1-C2u2=cte, est ce que le fait le dire que lorsque l'un se charge l'autre se décharge ce qui fais que cela se compense ? 
Salut,
1. Par une loi des mailles :
u1 + u2 - uR = 0
<=> -(q/C1 + q/C2) - Ri = 0 car les condensateurs sont en convention générateur.
<=> Ri + q(1/C1 + 1/C2) = 0
on dérive cette relation donc on a avec i = dq/dt
Rdi/dt + (1/C1 + 1/C2)i = 0
Que tu peux résoudre.
2. C1.u1 - C2.u2 = -C1.q/C1 + C2.q/C2 = -q + q = 0
donc C1.u1 = C2.u2
3. et 4. Il faut repartir de la loi des mailles et utiliser la relation de la question 2.

Salut, j'ai fini la question 2 et 3, j'ai lexpression de i(t) avec la condition initiale, mais la 3 je sais pas vraiment ou appliquer la loi des mailles



