Inscription / Connexion Nouveau Sujet
regime transitoire
Bonjour,
Je dois résoudre cet exercice, je me retrouve avec une équation différentielle du second ordre et je n'arrive pas a déterminer les constantes A et B
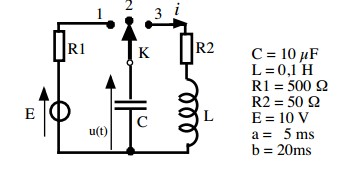
Au début, l'interrupteur est en position 2 et le condensateur n'est pas chargé. Puis, à
l'instant t=5 ms on met l'interrupteur en position 1; on attend jusqu'à t=20 ms puis on bascule
l'interrupteur en position 3.
Il faut tracer la courbe représentative de u(t)
Jusqu'a t=20 ms, le condensateur se charge, puis lorsque l'interrupteur est en position 3, j'applique la loi des mailles et j'obtient :
UR2+ Ldi/dt - Uc = 0
en posant  =L/R et Uc=u
=L/R et Uc=u
j'obtient une équation du type : d²u/dt + 1/ * du/dt -u = 0
* du/dt -u = 0
je trouve un discriminant poisitif, donc deux racines  = 905 et
= 905 et  =-1105
=-1105
d'où u(t) est de la forme : u(t)=Ae t+Be
t+Be t+K
t+K
Je bloque pour determiner A et B , on sait que a t=20ms, Uc = 9.5 V
merci d'avance.
En position 3 :
u - R2.i - L.di/dt = 0
i = -C du/dt
u + R2.C.du/dt + LC.d²u/dt² = 0
d²u/dt² + (R2/L).du/dt + (1/(LC)).u = 0
d²u/dt² + 500.du/dt + 10^6.u = 0
p² + 500p + 10^6 = 0 ---> p1 = -250 + 968i et p2 = -250 - 968i
u = e^(-250.t) * (A.sin(968.t) + B.cos(968.t))
A et B sont calculés à partir des conditions initiales u(0) = ... et i(0) = 0 ---> (du/dt)(0) = 0
...
Attention que l'équation ci-dessus considère t = 0 à l'instant du passsage de K en position 3.
Il faut donc penser à décaler le résultat de 20 ms ...
----
Sauf distraction. 
merci beaucoup de la réponse 
On a réussi a déterminer A et B , On a construit la courbe de U et on nous demande la valeur maximale de I et à quel instant ?
Il me semble que c'est lorsque U(t)=0 vaut 0, mais je crois qu'il y a un décalage car i est en avance ?
La tension sur C (juste au basculement de K de 1 à 3) est : u = 10.(1 - e^-3) = 9,5 V
-----
u = e^(-250.t) * (A.sin(968.t) + B.cos(968.t))
avec u(0) = 9,5 A et i(0) = 0 A
---> B = 9,5
u = e^(-250.t) * (A.sin(968.t) + 9,5.cos(968.t))
du/dt = -250.e^(-250.t).(A.sin(968.t) + 9,5.cos(968.t)) + e^(-250t)*(968.A.cos(968t) - 9,5*968.sin(968.t))
en t = 0 (20 ms pour l'énoncé) --->
-250 * 9,5 + 968.A = 0
A = 2,45
u(t) = e^(-250.t) * (2,45.sin(968.t) + 9,5.cos(968.t))
----
i(t) = -C.du/dt
On trouve donc facilement l'expression de i(t) (simple dérivée).
Et puis on étudie la fonction trouvée pour en trouver son max.
Il me semble qu'on arrive à imax = 0,068 A (arrondi) aux alentours de t = 1,36 ms après l'instant de commutation de K en position 3.
Mais je n'ai pas vraiment fait les calculs.
A vérifier. 


