Inscription / Connexion Nouveau Sujet
Régime transitoire
Bonjour, je bloque à la question 3, je ne vois pas comment détermines du/dt (0+). Et je ne vois pas non plus comment calculer le facteur de qualité, sachant qu'on est dans un circuit sans bobine ...
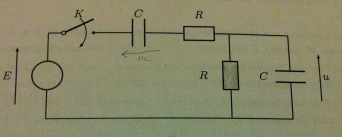
Voici le circuit :
Voici les questions :
On considère le circuit ci-dessus. Aux dates t < 0, l'interrupteur K est ouvert et un régime permanent dans lequel les condensateurs sont déchargés est établi. À la date t = 0, on ferme l'interrupteur.
1. Déterminer la valeur prise par u(t) une fois le nouveau régime permanent établi après fermeture de K.
2. Établir l'equation differentielle vérifiée u(t) pour t > 0. On posera τ = RC.
3. Déterminer les conditions initiales u(0+) et du/dt (0+).
4. Calculer le facteur de qualité Q associé à l'évolution u(t) dans le circuit. Comment peut-on qualifier le régime associé? En déduire l'expression de u(t) pour t > 0
Voici les résultats que j'ai trouvé pour les questions d'avant :
1. u(t->+inf) = 0
2. d^2(u)/dt^2 + (3/RC)*d(u)/dt + 1/(RC)^2 * u = 0
3. U(0+) = 0
Merci d'avance
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
1) loi des mailles -E +Uc+ Ri +Uc=0
régime permanent i=0
2) i=dq/dt et q=CU : équation différentielle
3) dériver U puis prendre t=0
Merci de votre réponse, mais :
1/ loi des mailles :
-E + Uk + Uc + Ri + u = 0 plutot, car l'interrupteur ouvert se comporte comme un dipôle "à air", non?
2/ i = C du/dt mais ensuite? Sachant que les deux condensateurs n'ont pas la même tension à leur bornes, comment trouvez-vous ce résultat?
3/ On n'a pas l'expression de u(t), donc on ne peut dériver u ...
1) Quand l'interrupteur est fermé Uk=0
2) bien vu, c'est moi qui ai écrit n'importe quoi
En raisonnant sur les intensités
i = i1 + i2
CdUc/dt = u/r + Cdu/dt
Uc = E-Ures-u
CdE/dt - CdUres/dt - CdUc/dt = uU/R + Cdu/dt
Ures = Ri =RCd²U/dt²
En remettant dans l'équation, je trouve une équation différentielle en d²U,dU,u
je trouve d^2(u)/dt^2 + (2/RC)*d(u)/dt + 1/(RC)^2 * u = 0
je dirais que Q =1/2
Désolé pour le temps perdu
1/ en régime permanent, on peut considerer le condensateur (entre l'interruptur fermé et la resistance) comme un interrupteur ouvert.
Donc en appliquant la loi des mailles,
E = Uc(t inf) + Ur(t inf) + U(t inf)
E = Uc(t inf) + Ri(t inf) + U(t inf)
Or i(t inf) = 0 donc U(t inf) = E - Uc(t inf)
Or Uc est inconnue ...
J'ai plutôt procédé comme ceci :
En régime permanent, les condensateurs sont assimilables à des interrupteurs ouverts, donc l'intensité i et i2 à leur branches est nulle. Donc en appliquant la loi des noeuds, on trouve i1(t inf) = 0.
Loi des mailles : U(t inf) = R i2(t inf) = 0
2/ On cherche l'équation différentielle vérifiée par u (tension aux bornes du condensateur de droite) et non Uc (tension aux bornes du condensateur à gauche)...
Mais je n'ai toujours pas trouvé du/dt (0+) et l'expression de la tension u(t) pour t > 0 du coup ...
si on prends Q=1/3 m'arrange car justement je coince sur la solution.
d^2u/dt^2 + 3/RC du/dt + 1/RC^2 u = 0 -> équation du second degré caractéristique.
x² +3 x + w² = 0, je pose w
x + w² = 0, je pose w =1/RC
=1/RC
 = 5
= 5 ²
²
la solution est A exp(x1.t) + Bexp(x2.t)
x = (-3


 )/2
)/2
pour trouver A et B à t=0 u(0)=0 et du-0)/dt =0 mais là aussi je bloque



