Inscription / Connexion Nouveau Sujet
Régime sinusoidale
Bonjour j'ai besoin de votre aide sur cette exercice assez basique:
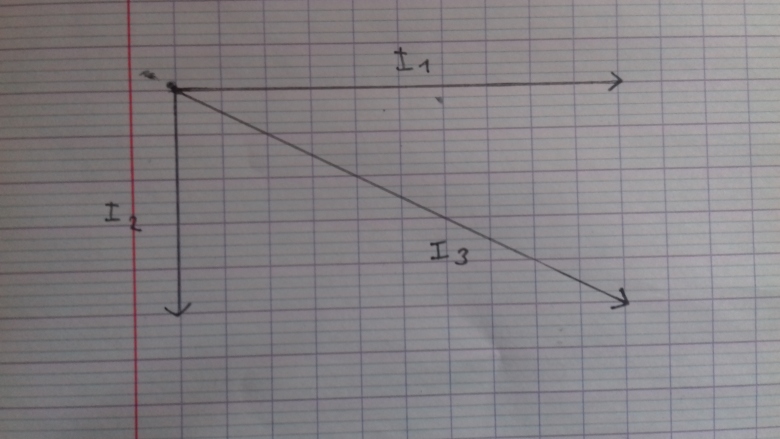
On considère le noeud de la figure 1 avec:
i1(t)=4 cos(ωt-60°)
i2(t)= 2 cos(ωt-150°)
(amplitude en mA)
Déterminer I3 (en précisant son amplitude et sa phase à l'origine des temps:
-Par la méthode des vecteurs de Fresnel
-En utilisant les nombres complexes.
Mon raisonnement:
Pour commencer je fait loi des noeuds:
I3= I1-I2
Pour le diagramme de Fresnel je prends comme axe de référence I1.
Maintenant pour le tracer je dois trouver le déphasage entre I1 et I2
Du coup est ce que ϕ 2/1 vaut -90° ?
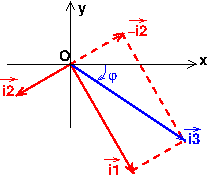
Peux-tu scanner et poster ici ton diagramme de Fresnel ?
Tu obtiens un résultat irréaliste. La différence i3=i1-i2 présenterait une amplitude maximale si i1 et (-i2) étaient en phase. L'amplitude serait alors la somme des amplitudes : 6mA. Tu dois donc obtenir une amplitude inférieure à 6mA.
Tu as fait cela juste par lecture graphique ou par un calcul tenant compte des différents vecteurs ? Tes résultats ne sont vraiment pas précis, surtout pour la phase.
Je ne connais pas les exigences de ton professeur mais a priori, il faut représenter les phases à la date zéro ; ainsi par exemple, le vecteur associé à i1 doit avoir un angle polaire de -60°.
Cela revient à faire tourner ta figure de 60° dans le sens des aiguilles d'une montre . Attention i3=i1-i2 et non i1+i2.
Bonsoir,
Exact on trouve comme module 2*sqrt(5) soit environ 4,5 mA avec Pythagore et la phase en degré est bien -60+arctan(1/2) soit environ -33°.
Bonsoir raptor666
Ton expression : " c'est exact " s'adresse à quoi exactement ?
D'autre part, fournir directement la réponse à un exercice n'est pas l'usage sur ce forum pour tout un tas de bonnes raisons.
Désolé. Avec ces posts croisés, je n'avais pas pris en compte la réponse concernant l'utilisation des complexes mais seulement ceux sur la méthode de Fresnel. Il faut donc oublié mon message précédent de 21h11.