Inscription / Connexion Nouveau Sujet
RDM poutres - coupures
Bonjour,
Je viens de commencer les poutres isostatiques en RDM, mais j'ai encore du mal a assimiler la notion de coupures au sein d'une poutre.
Le cours me dit qu'il faut couper à chaque fois que le chargement et les appuis changent.
Par exemple, dans la poutre suivante, dois-je couper uniquement en l/2 ?
Merci d'avance pour vos explications.
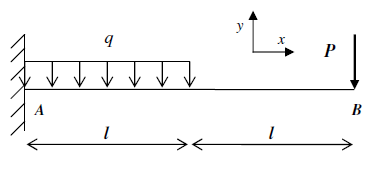
Salut,
Ce serait très long de tout te réexpliquer, je te renvoie donc à une explication illustrée faite par le passé :
Résistance Des Matériaux ; ingénieur
Concernant ton exo, la coupure fictive te permet d'expliciter le torseur de cohésion s'appliquant sur la poutre.
Le principe est simple, à l'image d'un scanner, tu balaies la poutre de B à A. A chaque fois que tu rencontres un effort, tu effectues une coupure fictive de telle sorte à expliquer le torseur en ce point.
Pour ton exercice, deux coupures sont à faire :
x 
[l ; 2l] :
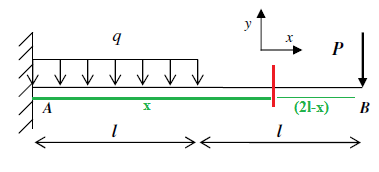
Seules deux composantes du torseur de cohésion sont non nulles :
* l'effort tranchant Ty = -P ("+ effort à droite", et vue que P est dans le sens contraire de y, c'est avec un signe -)
* le moment fléchissant Mfz = effort x bras de levier + sens parcouru dans le repère = -P(2l-x)
x [0 ; l]
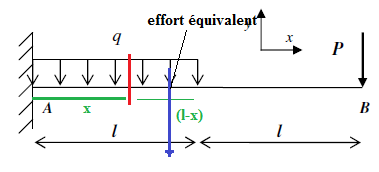
A toi de les exprimer
Salut,
Tout d'abord merci de ta réponse, elle m'a permis d'éclairer cette notion de coupure.
Je me suis donc lancé dans la résolution de l'exercice.
Calcul des appuis :
Les inconnues à calculer sont MA, FAY et FAX
FX = 0 
FAX = 0
FY = 0 FAY = P + ql
MA = 0 MA= ql²/2 + 2lP
Calcul des efforts :
Pour x [0,l] :
A gauche
dT / dx - q = 0 T(x) = qx + cte
Étude des conditions aux limites : T(x=0) = -FAY = -P - lq
D'où : T(x) = qx -P - lq
A droite
dT / dx - q = 0 T(x) = qx + cte'
Étude des conditions aux limites : T(x=l) = 0 (L'effort de charge q doit il être considéré dans l'effort tranchant en x=l ?)
D'où : T(x) = qx -ql
Je rencontre ici un problème : la courbe de l'effort tranchant T(x) est censé être continue , or ici ce n'est pas le cas sur cette portion (le P ne devrait pas être présent dans l'expression de T(x) à gauche.
Avant de continuer j'aimerais donc connaitre mon erreur et la rectifier.
Merci de ton aide 
Déjà, je suis content de voir que tu fais la distinction entre à gauche et à droite de la coupure.
___________________________________________________________
Mais deux calculs doivent aboutir au même résultat si tu regardes à gauche ou à droite de la coupure, avec la règle suivante :
* Torseur de cohésion = "+ ce qui est à droite de la coupure"
* Torseur de cohésion = "- ce qui est à gauche de la coupure"
___________________________________________________________
Pour ma part, dans la première coupure que je t'ai explicitée la fois précédente, j'ai fait mon calcul en faisant une coupure pour x
[l : 2l] et en appliquant Torseur de cohésion = "+ ce qui est à droite de la coupure" (mais si j'avais regardé ce qui se passait à gauche de la coupure, ça aurait été la même chose) :
(ma coupure sur mon premier schéma était au niveau du trait rouge :
Seules deux composantes du torseur de cohésion sont non nulles :
* l'effort tranchant Ty = -P ("+ effort à droite", et vue que P est dans le sens contraire de y, c'est avec un signe -)
* le moment fléchissant Mfz = effort x bras de levier + sens parcouru dans le repère = -P(2l-x)
Ensuite, étudie le cas x
[0 ; l]
Je t'avais déjà fourni des éléments de réflexion. Comme pour la coupure précédente, P va intervenir, mais comme tu peux le constater, il y a dans la coupure (tjs le trait rouge) également un bout de la répartition linéique d'effort. Il faut donc en tenir compte dans tes expressions pour Ty et Mfz en te disant (par une intégrale immédiate) que ce bout de répartition est équivalent à un effort ponctuel situé au centre de gravité du rectangle de longueur (l-x) et de largueur q.
Donc Ty = -P - q.(l-x)
Remarque importante : tu vérifies la continuité avec la coupure précédente puisqu'en x = l, on a Ty = -P
Essaie de trouver Mfz
Concernant la partie [0,l] je n'ai pas très bien compris la fin de ton post, lorsqu'il s'agit de l'équivalence à un effort ponctuel (le point d'application de cet effort est il au centre de gravité du rectangle ? )
Pour résumer, j'avais trouvé une valeur de T(x) à gauche : T(x) = qx -P - ql = -P -q(x-l)
Jusque là j'ai compris le raisonnement (utiliser les conditions aux limites en x=0 pour trouver la constante)
Mais pour le calcul de T(x) à droite, je ne comprend pas en quel point il faut étudier les conditions aux limites (instinctivement, j'aurais étudié au point x=l mais je ne comprend pas comment exprimer l'effort tranchant en ce point)
En somme, je ne comprend pas comment tu arrives à cette formule de T(x) pour la partie droite
(Désolé pour le double post)
Après mure réflexion je me dit qu'on a pas besoin de connaitre les conditions (effort tranchant et moment fléchissant) au point x=l.
En effet, pour [0, l] ou pour [l, 2l] l'étude de la partie gauche ou de la partie droite suffit (on s'aide seulement des conditions en A et B).
Sur [0,l], j'obtiens pour le moment :
M(x) = -qx² / 2 + Px + qlx + cte
L'étude des conditions aux limites en x=2l me donne : cte = MA
Soit M(x) = -qx² / 2 + Px + qlx + MA
Si tu veux, je préfère regarder à droite car cela m'évite dans ce cas de chercher les efforts aux liaisons 
.
Mais encore une fois mon expression est correcte et en faisant "- ce qui est à gauche", tu dois aboutir au même résultat pour x entre l et 2l pour Ty.
Ensuite pour mon expression de Mfz, tu dois vérifier la condition Mfz(2l) = 0, ce qui est bien le cas avec mon expression
Pour x entre 0 et l,
Mfx = -P(2l-x) - (l-x)/2.q.(l-x) = -P(2l-x) - q.(l-x)²/2
Vérification continuité de Mfz en x = l :
Mfz(l) = -P.l dans les deux cas, ce qui est rassurant
J'arrive aux même résultats que toi, donc c'est tout bon
Je te remercie pour toutes tes explications, ça fait vraiment plaisir d'être soutenu comme ça !
En te souhaitant une bonne continuation, et peut-être à une prochaine fois pour un autre problème !
Annuler
connectez vous