Inscription / Connexion Nouveau Sujet
RDM poutre droite
Bonjour,
Je tente de résoudre un exercice de RDM. Il s'agit d'une poutre avec appuis simple, et on me demande l'effort tranchant et le moment fléchissant.
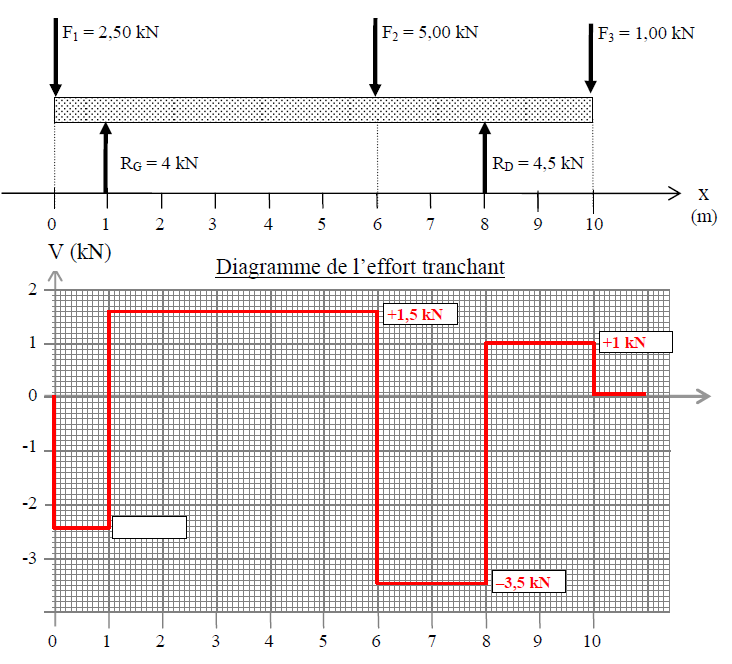
Voici la poutre en question, avec le diagramme correspondant donné par la correction.
Seulement je rencontre un problème dès la première coupure (zone de x=0 à x=1). En utilisant les équations du cours je trouve :
A gauche : dT / dx = 0  T(x) = cte.
T(x) = cte.
Condition aux limites en x=0 : T(x=0) = -F1 = -2.5.
Je retrouve donc la même valeur que la correction.
Mais par curiosité, j'ai voulu utiliser la partie droite de cette coupure. Donc je regarde les conditions aux limites en x=1, ce qui me donne : T(x) = Rg = 4. J'obtiens donc une valeur différente, alors qu'elle devrait être identique sur toute la portion (x=0, x=1).
Pourriez vous m'éclairer sur ce petit problème ?
Merci d'avance 
Salut,
La fonction de l'effort tranchant est discontinue,
Qaund la dérivée de la fonction est définie alors dT/dx=0 mais comme la fonction est discontinue il existe des point où elle n'est pas définie
C'est comme pour la fonction h(x)=1/x elle est strictement décroissante sur  -* et
-* et  +*
+*
mais il est faux d'en déduire qu'elle est strictement décroissante sur  * car elle est discontinue en 0.
* car elle est discontinue en 0.
oui les traits verticaux n'existent pas sinon ce n'est plus une fonction.
en effet, une fonction n'admet qu'une image par abscisse
D'accord, dois-je donc comprendre qu'il ne faut pas étudier les conditions aux limites au niveau des appuis de ma poutre ?
tu peux le faire mais tu ne dois pas t'étonner que les limites à droite et à gauche sont différentes
Entendu, j'y penserai à l'avenir.
Autre souci, lorsque j'étudie la portion (x=1; x=6), j'utilise encore les équations d'équilibre :
dT/dx = 0  T(x) = cte
T(x) = cte
En étudiant les conditions au limites en x=6, j'ai : T(x=6) = -F2 = -5
D'où T(x) = -5 sur cette portion.
Or je tombe en désaccord avec la correction, saurais tu me dire pourquoi ?
Je te remercie pour ton attention.


