Inscription / Connexion Nouveau Sujet
Rdm : exercice
Bjr a tous.j ai un exo sur la RDM. Puis je le propose pour qu on le traite ensemble?merci de repondre .cordialement.
Salut,
Si tu ne postes pas l'exercice en question (recopier l'énoncé et poster l'image avec le bouton "Img") on va avoir du mal à t'aider.
Donne-nous également tes pistes de réflexion.

Bjr Gbm.
Voici le sujet en question:
Un poteau de section constante  , de hauteur h supporte a sa partie superieure une charge p appliquee au centre de gravite de la section.
, de hauteur h supporte a sa partie superieure une charge p appliquee au centre de gravite de la section.
Entre son sommet et sa base, outre son poids propre , I'll recoit une surcharge d intensite p au metre courant de hauteur .
Determiner l aire de la section  pour que la contrainte a la base soit egale R bars.
pour que la contrainte a la base soit egale R bars.
La masse volumique du materiau est egale a  kg /m3 et le coefficient d elasticite est egal a E bars.
kg /m3 et le coefficient d elasticite est egal a E bars.
Calculer le raccourcissement du poteau sous l action des charges et surcharges auxquelles I'll est soumis.
Application numerique:
P=50.000 daN ; R= 65 bars  =2500 kg/m3
=2500 kg/m3
E=2x10 exp 5 ;p= 5.000 daN/m ; h = 10 m.
J ajoute que je suis en formation de l ingenierie du genie civil depuis la chine.
Merci de repondre.cordialement.
*** message déplacé ***
Salut,
Première chose : étant donné que tu avais déjà créé un topic pour ton problème, ne reposte pas un énoncé dans un deuxième topic, cela s'apparente à du multipost, et c'est interdit sur ce forum.
Ensuite, as-tu commencé par un schéma de la situation ?
Utilise Paint pour le dessiner proprement (avec toutes les données de l'énoncé) et utilise le bouton "Img" pour le poster (bouton juste en-dessous du cadre où tu écris)
Bjr.le probleme je ne sais pas comme est la forme du poteau.je ne sais pas si c est un poteau cylindrique ou rectangulaire.voila pkoi je ne sais pas ou commencer
bjr Gbm,compte tenu du decalage horaire j ai pas pu vs repondre.
aussi j utilise la tablette donc cela ne me donne pas la possibilite de faire des dessins 2 D .par contre je peux le faire a la main et expedie.merci pour votre comprehension.
retrouvez en fichier attache le schema.merciii.
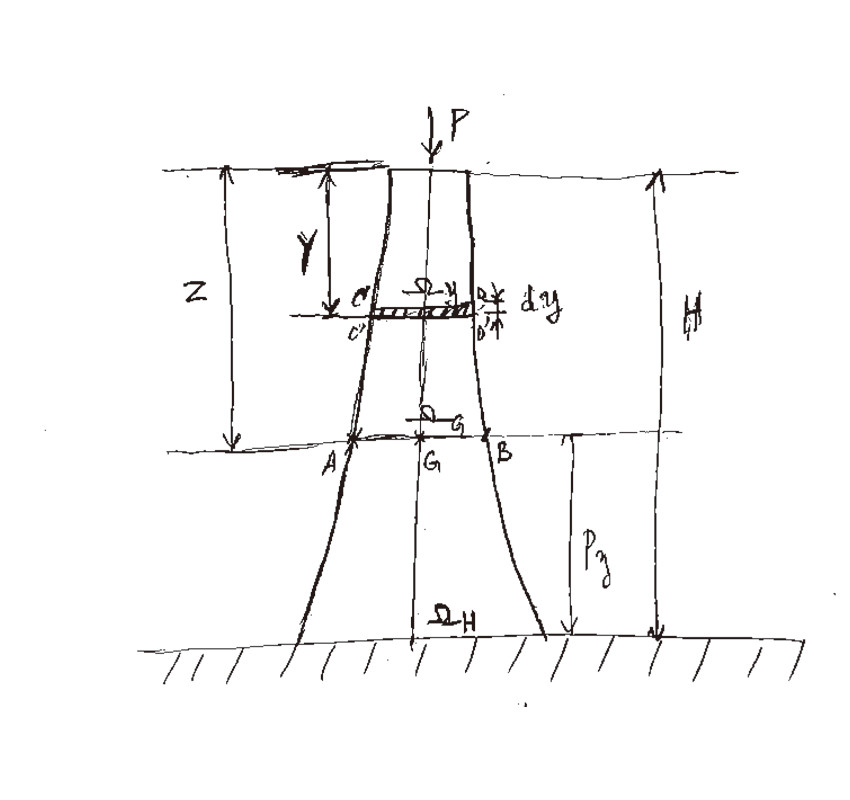
*** message déplacé ***
Relis ton énoncé, il indique bien "section constante", ce qui simplifie GRANDEMENT ton exercice.
 .
.
Une fois que tu auras refait le schéma, quelles notions du cours de RDM peuvent t'aider ?
Quelles hypothèses ?
Bjr.je vais bien reflechir la dessus et te revenir.il. y a un exo semblable ou on parle de section constante et la figure se presente comme le schema.bon je vais voir et vs faire signe.merci.
Bjr Gbm, je pense que cet exercice n a pas besoin de schema specifique.on doit appliquer la relation de hooke du moment ou la section est constante.je t envoie ma demarche.
 =F/S=50.000daN/65=769,23daN/cm2
=F/S=50.000daN/65=769,23daN/cm2
Ensuite pour trouver l allongement , je tiens compte de la pesanteur et et de la masse volumique de la section.ce qui donne:
 L=1/ExS(F+(
L=1/ExS(F+( xgxSxH)/2.
xgxSxH)/2.
Est ce que la demarche est juste?merci de repondre .cordialement.
Re,
Dsl, je travaille à côté du passe-temps qu'est l' ...
...
Voici une proposition de schéma pour tenter de coller au mieux à l'énoncé :
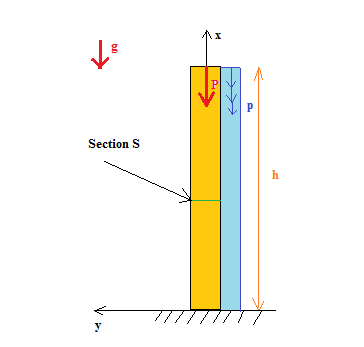
P est la charge appliquée au sommet du poteau, au centre de gravité de la section (en rouge) ;
p est la répartition linéaire tout au long de la poutre (je l'ai représenté en bleu à droite plus plus de lisibilité, mais elle s'applique au centre de gravité de chaque section de la poutre, sur toute sa longueur) ;
Enfin, la poutre est soumise à son propre poids tout au long de la poutre.
Pour simplifier le problème, je te conseillerai d'écrire le torseur de cohésion pour chaque sollicitation, indépendamment des unes des autres.
Tu trouveras à la fin l'effort normal appliqué à l'ensemble de la poutre (trace les diagrammes pour chaque effort, puis pour l'effort total).
Ensuite, je ne comprends pas ton raisonnement. Tu ne connais pas la section, puisque c'est justement ce que tu cherches.
Je suis d'accord sur la formule de la contrainte normale appliquée sur une abscisse x de cette poutre :
avec l'effort normal total.
On cherche S telle que , soit S = ?
Attention : x = 0 correspond à l'abscisse à la base de la poutre (au niveau de l'encastrement).

Bjr Gbm, voila je te reviens rapidement pour te proposer ma demarche si elle est bonne?
Reaction de l encastrement  Ray;May ) au point de l encastrement.ce qui representerai le torseur en ce point .
Ray;May ) au point de l encastrement.ce qui representerai le torseur en ce point .
Ensuite on isole la poutre.
Inventaire des forces:
La reaction Rax
Le poids p
La pesanteur g
L effort d encastrement a la base :Ma.
Je dois trouver l expression de Ray et Ma au point A c a d a la base.
Les cordonnees me donneront le torseur .comment faire ensuite pour trouver l aire .
Seulement  =Ma/I
=Ma/I
I:moment d inertie de la section.merci de repondre cordialement.
C est cela mon probleme.les diagrammes.je ne sais pas comment elabore?par contre je peux trouver les expressions analytiques du moment et de la reaction.je pense que c est un peu complexe pour moi.
Ce qui me surprends un peu : tu as eu un cours sur le sujet  ?
?
Après, si tu arrives à trouver l'effort normal au point d'encastrement, pourquoi pas.
Bjr Gbm, excuses moi pour ce retard.en fait je ne comprends pas bien l exercice voila pkoi je l ai propose pour plus d explication.le cours est bien clair mais I'll y a des non dit dans ce qu ils nous donne.je traite tjrs mes devoirs seul.mais celui la je ne comprend pas bien.merci de repondre cordialement.
Ta poutre est soumise à trois types d'effort :
* son propre poids,
* à sa partie supérieure une charge P appliquée au centre de gravite de la section,
* une surcharge d intensité p au mètre courant de hauteur,
Pour te simplifier, je te propose de décomposer l'analyse de la façon qui suit :
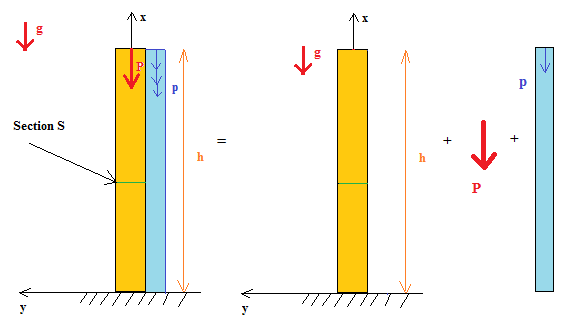
Tu peux de cette façon trouver les trois efforts normaux appliqués à la poutre et les sommet pour en revenir à ton pb.
Cas 1 : poutre soumise à son propre poids : = masse du poteau à l'abscisse x =
= volume de la poutre à l'axe x =
masse volumique de la poutre
Cas 2 : effort ajouté au sommet de la poutre :
N_2(x) = -P
Cas 3 : effort le long du poteau
Même méthode que pour le cas 1.
Donc
Tu cherches l'effort à ma base, donc en soit
à calculer.
Ensuite comme tu l'as dit, la contrainte appliquée à la base vaut :
soit

N1(0)= xhxgx
xhxgx
N2(0)= - p =50.000 daN
N3(0)=meme valeur que N1(0).
N1(0)=2500 x x10x9,81=245250
x10x9,81=245250 
N2(0)=-50000 daN/m
N3(0)=N1(0) donc
N(0)=490500 - 50000
- 50000
Verifies mes expressions stp.
Attention,
Je t'ai écrit que pour le cas 1 et 3, c'est la même méthode, PAS la même valeur.
D'un côté tu es soumis au champ de pesanteur, de l'autre à une charge répartie p.
Bjr Gbm.je recapitule donc.
N1(0)= xh a l abscisse x=0
xh a l abscisse x=0
N2(0)=-p
N3(0)=-pxh a l abscisse x=0 charge uniformement repartie
Valeur algebrique :
N1(0)=2500x10x
N2(0)=-50.000 daN
N3(0)=-50000 daN
N(0)=-50.000 daN-50.000 daN +2500x10x
N(0)=-100.000 +250 
 xL=(N(0)/(Ex
xL=(N(0)/(Ex )
)
=0,028 m
=2,8 cm
Voici ce que je trouve apres ton aide.merci bcp .aussi verifie pour moi.cordialement.
La méthode semble comprise  !
!
Je te fais confiance pour les applications numériques, l'essentiel pour moi est que tu aies assimilé les astuces de décomposition des torseurs de cohésion
Bjr Gbm.je te reviens encore.
Est ce que le N3(x)=-px(h-x)
A l abscisse x=0, N(0)=-pxh.
Est ce vrai?
Quand je calcule je trouve l aire de la section un peu trop petit.
Soit  =0,40 m2.
=0,40 m2.
Est ce qu I'll. N y a pas un probleme de convertion?
Aussi pour l allongement j ai utilise la formule :
 L=(N(0)xh)/ExS).
L=(N(0)xh)/ExS).
S I'll te plait verifies pour moi .merci bcp pour ta disponibilite.
Cordialement.
Bjr Gbm.je pense qu I'll doit avoir une petite erreur dans l expression de N3(x).
Tu as ecris N3(x)=-p.(h-x)/x. Ce qui n est serait pas correcte pour une valeur de x a l abscisse 0.
Pour moi comme la charge est uniformement repartie comme tu me l as bien explique, on doit peut avoir l expression suivante :
N(x)=-p.(h-x)/2.aussi email pour conract.merci de repondre cordialement.
Oui ! Tu as raison, j'ai fait une faute d'inattention dans ce cas.
N3(0) = -ph --> OK
Au temps pour moi 
La méthode littérale est désormais correcte, pour l'application numérique, si tu mets tout en unité SI ça devrait être bon.
Si S = 0,40 m² --> S = 4000 cm² !
Cela fait presque une poutre de 63 cm x 63 cm quand même.
Il faudrait dans l'absolu que je refasse le calcul, mais comme tu l'as compris je fais un saut ultra rapide à chaque fois sur l'île et la modération prend du temps  .
.
Bjr Gbm.c est vraiment correcte.merci pour ta participation.peut on encore poursuivre dans les theories de poutre a encorbeillement ou encore poutre console.merci de repondre .bien sincerement.
Ouf ! On est arrivé jusqu'au bout  !
!
Pour les poutres à console, c'est celle avec un encastrement c'est ça ? A la rigueur tu peux créer un NOUVEAU topic pour cette dernière.
En revanche pour la poutre à encorbellement, je ne suis plus sûr d'avoir les compétences, ce n'est pas ma spécialisation :/.
Bjr Gbm.c est une poutre a console sur appui simple mais avec encorbellement de part et d autre.merci.cordialement.
Ecoute, poste toujours dans un nouveau topic avec un schéma cette fois-ci.
Si je n'y réponds pas c'est que j'estimerai ne pas être le meilleur interlocuteur pour.



