Inscription / Connexion Nouveau Sujet
RC série
Bonjour à tous,
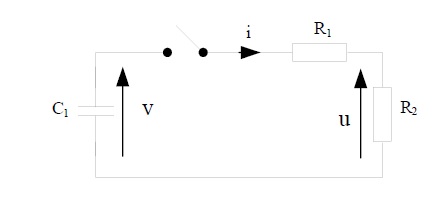
On considère que le condensateur est déjà chargé et on ferme l'interrupteur.
Dans le schéma, j'ai trouvé l'expression de v, et je dois en déduire l'expression de v.
La correction donne v = R2/(R1+R2) * E* e(-t/to) avec to = C1*(R1+R2).
Moi, j'avais choisis d'utiliser la loi des mailles :
u=v-R*i. Au début, i=0 car v ne varie pas car le condesateur est chargé, donc u=E.
Je comprends la méthode de la correction, mais je ne comprends pas pourquoi la mienne ne marche pas.
Une idée ? 
C'est parce que i n'est pas nul.
La tension V aux bornes du condensateur ne change pas au début.
Le courant qui circule vaut V/R.
Oui, v ne change pas au début. donc dv/dt =0 donc i=cdv/dt =0, non?
Sinon, selon vous, l'idée de la méthode des mailles est bonnes ? (I nest pas donnée dans l'énnoncé)
difficile de te répondre (tu peux me tutoyer toi aussi) sans le schema. V ne change pas à t=0+, mais ça ne signifie pas qu'elle ne commence pas à changer et donc que dv/dt soit non nul. Il n'y a juste pas de discontinuité de tension.
v - R1.i - R2.i = 0
i = - C1.dV/dt
v - (R1+R2).i = 0
i = - C1.dV/dt
v + (R1+R2).C1.dV/dt = 0
dv/dt + v/(C1(R1+R2)) = 0
---
La résolution de cette équation difféentielle donne :
v = K.e^(-t/(C1(R1+R2)))
En posant to = C1*(R1+R2), il vient :
v = K.e^(-t/to)
La valeur de K se trouve par une condition initiale ... qui n'est pas donnée dans l'énoncé fourni.
-----
Sauf distraction. 
Euhh. Oui, là on obtient l'équa diff de base, mais on doit trouver l'évolution de u (j'ai fait une faute de frappe dans mon premier message), à partir de là.
Et donc je me demande si il est possible d'utiliser la loi des mailles, plutot que de faire v/(R1+R2) * R2 ?
Oui, tu peux ecrire que u=v-R1i=v-R1Cdv/dt
avec l'expression de v que J-P t'a donnée, tu vas y arriver.
Il est juste dommage de faire si compliqué quand la règles du diviseur de tension est applicable.