Inscription / Connexion Nouveau Sujet
Question sur les projections
Bonjour,
Je voudrais vous demander de m'expliquer quelques chose que je ne comprend pas et ça me prend la tête lol!
En fait c'est l'histoire des projection...
Prenons le cas de la chute libre verticale sans vitesse initiale.
Je laisse tomber mon objet d'une hauteur h. Je peux dire que d'après la seconde loi de Newton,
m =m
=m donc
donc  =
=
L'axe que j'ai choisis est l'axe (Oz) orienté vers le haut. Donc si je projette  sur (Oz) j'ai bien
sur (Oz) j'ai bien  =-g
=-g Donc az=-g
Donc az=-g
Mais si j'avais voulu projeter  sur (Oz), j'aurais eu -az
sur (Oz), j'aurais eu -az =-g
=-g donx -a=-g et donc a=g
donx -a=-g et donc a=g
En faite mon incompréhension vient du faite que je n'arrive pas à discerner composante de projection... Et j'ai ce problème avec les forces de frottement qui sont égale à -kv et avec tout ce qui est énergie potentielle...
Je comprend tout mes cours de prépa... mais c'est seulement ce point qui vient tout me bloquer.
Alors si queslqu'un se sentait de m'expliquer concrètement pour que je ecomprennes une fois pour toute je lui serai très reconnaissant...
Merci beaucoup à vous
Bonne soirée 
Bonjour,
Je voudrais vous demander de m'expliquer quelques chose que je ne comprend pas et ça me prend la tête lol!
En fait c'est l'histoire des projection...
Prenons le cas de la chute libre verticale sans vitesse initiale.
Je laisse tomber mon objet d'une hauteur h. Je peux dire que d'après la seconde loi de Newton,
L'axe que j'ai choisis est l'axe (Oz) orienté vers le haut. Donc si je projette sur (Oz) j'ai bien a=-g\vec{k} Donc az=-g
Mais si j'avais voulu projeter sur (Oz), j'aurais eu
donc -a=-g et donc a=g
En faite mon incompréhension vient du faite que je n'arrive pas à discerner composante et projection... Et j'ai ce problème avec les forces de frottement qui sont égale à -kv et avec tout ce qui est énergie potentielle...
Je comprend tout mes cours de prépa... mais c'est seulement ce point qui vient tout me bloquer.
Alors si quelqu'un se sentait de m'expliquer concrètement pour que je ecomprennes une fois pour toute je lui serai très reconnaissant...
Merci beaucoup à vous
Bonne soirée
Bonjour,
Un axe :
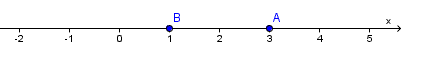
C'est la longueur du segment AB
C'est la mesure algébrique du segment AB
________________
donc
les normes (toujours positives, comme les longueurs) des vecteurs sont égales
Dans le repère (O,  ,
,  ,
,  ) les vecteurs
) les vecteurs et
ont pour coordonnées ax, ay, az et gx, gy, gz tels que :
Les composantes de et de
dans la base (
 ,
,  ,
,  ) sont les vecteurs :
) sont les vecteurs :
pour : ax.
 , ay.
, ay. et az.
et az.
et pour : gx.
 , gy.
, gy. et gz.
et gz.
Si tu orientes l'axe Oz vers le haut, alors les coordonnées az et gz sont égales et négatives.

Merci beaucoup pour ta réponse.
Donc si j'en crois ta dernière phrase, on peut donc dire que ... Donc -az=-gz donc az=gz or la réponse correct est az=-g..
Est-ce que tu vois ce que je veux dire ?
Tout dépend de ce que tu nommes g !
si est la norme (positive) de
alors, bien sûr, la coordonnée gz = az = - g

C'est dingue que je ne comprennes pas ça ... ça m'enerve !!
parce que pour moi gz=g ...
Je ne vois pas la différence. J'ai compris tes explications c'est ça le pire ! Comment est-ce que gz et az peuvent ils être négatif...
La coordonnée gz est égale au produit scalaire
si l'axe est orienté vers le haut, comme le vecteur accélération de la pesanteur est orienté vers le bas, aucun doute, le produit scalaire est négatif et la coordonnée selon l'axe Oz également.
Idem pour la coordonnée az qui est égale au produit scalaire

Impossible de répondre à une phrase qui n'est pas terminée.
Si tu veux des explications claires il faut peut-être que tu sois clair(e) toi aussi.

Ah oui !
J'ai compris.
Comme le vecteur g et le vecteur k sont colinéaire de sens inverse, il y a un cos( ) qui les sépare, donx gz=|g|*|k|*cos(pi)
) qui les sépare, donx gz=|g|*|k|*cos(pi)
gonc gz=-9.81=-g et comme az=gz on peut dire que az=-9.81=-g ?
Merci beaucoup de ton temps que tu m'as accordé 


