Inscription / Connexion Nouveau Sujet
Question sur le bras de levier
Bonjour!
Voila j'ai une question qui m'est venu en rêve ( lol):
on a tous remarquer que lorsque l'on porte un objet de masse,M, avec les bras TENDUS, cela est beaucoup plus difficile de tenir l'objet que si on avait les bras rapprochés du corps.
Alors je me suis dit qu'il devait avoir une explication physique à ça: plus le bras de levier de la force F que l'on applique pour tenir l'objet est elevée, plus on aura du mal à tenir cet objet .
Donc j'ai pris mes stylos et puis j'ai calculer la position d'équilibre de l'objet de masse M, située à une distance d de notre corps: F = 0 (1)
F = 0 (1)
et aussi  M(F) =0 (où M(F) c'est le moment de la force . (2)
M(F) =0 (où M(F) c'est le moment de la force . (2)
donc puisque il y a le poids, P et la force F qui est appliqué à l'objet : ( j'utilise le repère cartésien )
tout calcul fait on obtient:
(1) donne: F=mg (en norme)
(2) donne : dF=mgd ( en norme)
Donc on obtient F=mg dans les 2 cas ce qui est logique pour avoir équilibre de l'objet.
En revanche je ne comprend pas pourquoi la distance d n'intervient pas dans l'expression de F... puisque logiquement si d augmente alors il va me falloir plus de force F pour garder l'objet en equilibre non?
merci pour vos futurs réponses ( please vous moquez pas de moi ^^ lol )
***Forum changé***
Bonjour,
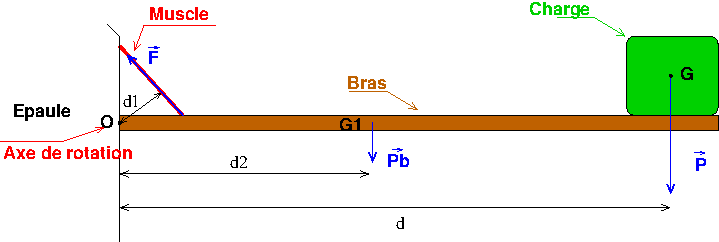
Une modélisation très simplifié voire grossière, pourrait être la suivante (voir schéma) :
1 : le bras assimilé à un cylindre horizontal mobile autour d'un axe passant par le point O de l'épaule et perpendiculaire au plan de figure. Son poids est Pd, son centre de gravité est à la distance d1 de O.
2 : une surcharge de poids P dont le centre de gravité G est à la distance d du point O.
3 : les muscles reliant le bras à l'épaule qui exerce une force F conformément au schéma (c'est là que la modélisation est la plus grossière).
Ecrire que l'ensemble {bras , charge} ne tourne pas autour de l'axe de rotation conduit à l'égalité suivante (théorème des moments) :
soit :
On voit bien que, plus le bras de levier d est important, plus la force musculaire F est intense.
Encore une fois : il s'agit d'une modélisation très simplifiée et la figure n'est pas à l'échelle... Je n'ai pas modélisé l'action de l'épaule sur le bras au niveau de l'axe de rotation puisque le moment de cette action (calculé au point O) est nul.