Pour être plus précis je veux savoir comment s'y prendre quand t'on a une fonction d'onde dépendant, en plus des coordonnées spatiales, du temps également.

Hello

Il y a sans doute une coquille dans l'expression de que tu voulais formuler comme:

(x,t)=Asin(ax)e^-iEt/h

Petit rappel de ce qui est sans doute dans ton cours(on redémontreras 3) si tu en éprouves le besoin):

1)Equation de Schroedinger => fournit la loi temporelle d'une fonction d'onde
2) l'Hamiltonien admet des fonctions propres stationnaires
3) Si (x) est fonction propre pour la valeur propre E, alors (x,t)=(x)e^-iEt/h décrit l'évolution temporelle de la fonction propre

La bonne nouvelle dans tout cela c'est que:

|(x,t)|² = |(x)|²

Te voici remis en selle?  (Il serait peut être bon de restituer le contexte, l'exercice pour pouvoir t'aider de manière concrète et non pas simplement rappeler du cours)

Bon on m'as donné une fonction
(x,t)=Asin(2πx/a)exp(-iEt/h)
A la première question on me demande de calculer la constante A.
Pour cela, j'utilise la condition de normalisation
||²dx. Mon problème est que comme cette fonction dépend de deux variable, comment vais je l'intégrer ??

Pardon j'ai commise une petite erreur
Condition de normalisation
||²dx=1.
Comme la fonction dépend de plusieurs variable, on aura pas aussi un dt dans cette expression ??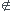
Pour conclure
comment intégrer cette fonction ??

Hum hum...

Tu n'as peut être pas lu attentivement mon précédent msg:



Posons



Donc



Et



Donc à un instant t (quelconque):



Tu remarqueras que:

- dans la question posée, on de demande d'intégrer suivant "dx" ie la position dans le domaine, et pas d'intégrer suivant le temps!
- donc tu traites la fonction comme tu traitais jusqu'à présent la fonction :

Bon d'après l'énoncé
(x,t)=Asin(2πx/a)exp(-iEt/h) pour |x|=a/2
(x,t)=0 ailleurs

C'est rassurant ... le domaine est borné  (la fonction était divergente dans l'ensemble de l'espace)

Il s'agit donc d'intégrer entre    et  

A toi?

Merci bien dirac.

De rien. Tu dois trouver qlq chose comme

Pour redonner son sens physique à ton exercice: nous sommes dans le cas d'une particule dans un puits de potentiel infini