désolé j'ai oublié le schéma

Bonjour,

1- précisez votre raisonnement
2- vous avez du voir en cours l'écriture "canonique" des fonction de transfert. Il suffit d'identifier.
2 bis- ou alors repasser dans le domaine temporel et de nouveau identifier.

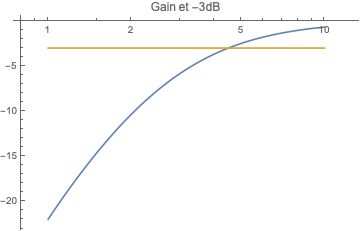
2ter- tracé le diagramme de Bode, comment repère-t-on la pulsation de coupure ?

Dernière chose : quand vous parlez de pulsation de coupure, vous parlez de pulsation caractéristique ou de bande passante à -3dB ?  

1)
en basse fréquence la bobine se comporte comme un fil donc Vs = 0

en haute fréquence la bobine se comporte comme un interrupteur ouvert on obtiens Vs = Ve

conclusion ce filtre est un passe haut

2) je comprends pas

Voici l'écriture canonique des filtres passe haut de second ordre




je comprends pas en comment identifier permet de trouver la pulsation de coupure

Par identification, on trouve immédiatement d'où puisque vous connaissez votre x.
Problème avec cette méthode, très rapide, elle donne la pulsation caractéristique, qui est la grandeur utile.

Si le texte veut la pulsation de coupure à -3dB, là c'est plus tordu et il y a du calcul à effectuer qui consiste à traduire ce -3dB. Donc quelle est la définition pour H de -3dB ?

Remarque : OK pour la justification.

c'est | H(jx) | = 1

Pulsation de coupure à -3 dB.

désolé

c'est la pulsation pour laquelle G(c) = G()/ 2

Plutot

G () = G(w)max / 2

Cette fois c'est correct, il n'y a plus qu'à faire le calcul.

A un détail près ce n'est pas le maximum, mais le gain dans la zone passante (ici HF).

le gain de la zone passante en HF est x² comment je fais ?

et pourquoi en haute frequence ?

En haute fréquence parce que l'on a un passe-haut.
Dans le cas général, cela serait le gain dans la bande passante.

je comprends pas

Comme réponse à la question 1, vous avez écrit que en HF Vs=Ve donc le gain vaut ?

il vaut 1

donc = 1 /  2

ignorez mon dernier message.

je n'arrive pas à trouver

Donc en effet et que vaut

c'est quoi abs ?

je pense que c'est la valeur absolue

C'est presque cela : il manque un carré à , et comme cela vaut , x= ?

Il suffira de resoudre

  donc j'obtiens x = 0,374

Merci beaucoup pour votre aide

Attention vous avez oublié le numérateur.

on a ca : =

j'ai utilisé ca pour calculer le x

Vous avez dit le 07-12-20 à 18:09 que la gain valait 1 dans la bande passante, donc il n'y a pas de x² à droite.

oui c'est vrai.

Mais il ya quelque chose de bizarre lorsque je mets 1 quand j'essaie de calculer le x c'est impossible

Ah si je trouve x = 4,128

Vous êtes sûr ? Je trouve 2,67

j'ai du faire une erreur de calcul.

Mais ce qui est bizarre c'est que dans le cour c'est la premiere réponse j'ai donné qu'ils ont trouvé comment cela se fait il ?

Vous voulez dire que dans le cours il y a indiqué x=0,374 à la coupure ?

exactement

parce qu'il ont trouvé

ils avaient plaqué et je voulais démontrer donc ils ont fait une erreur dans le livre ?

Si la fonction de transfert est bien   voici le diagramme de Bode et la limite à -3dB.

Vous êtes sûr que c'est bien le même exo, parce qu'avec un passe-bas (donc des capacités), on trouve bien 0,374

exactement

ils ont trouvé  passe haut et la pulsation de coupure 0,374

Donc voir le diagramme !

j'ai montré il y a bel et bien une erreur merci monsieur on trouve 2,67