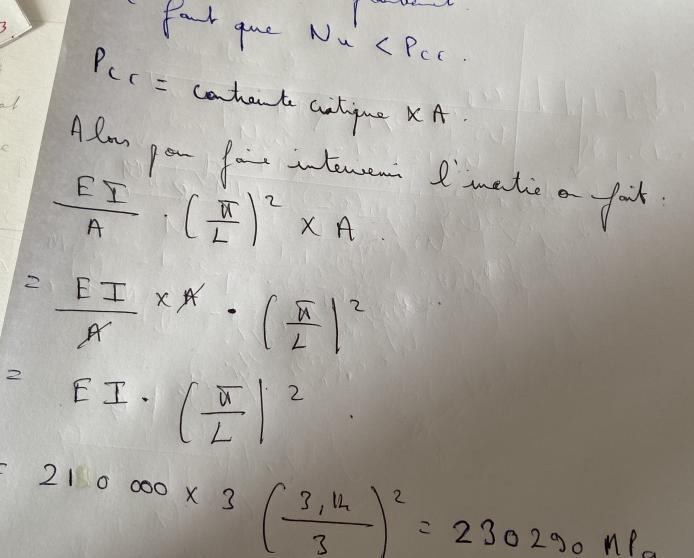Inscription / Connexion Nouveau Sujet
Je vais te proposer une méthode semi-analytique à opérer sur chaque tronçon de la poutre.
Premier cas : coupure fictive d'abscisse x  [2c ; 2c+e ]
[2c ; 2c+e ]
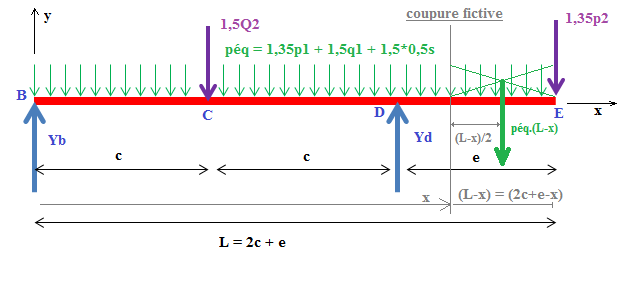
Je vais regarder ce qui est à droite de la coupure (plus simple dans ce cas de figure), j'ajouterai donc un signe "+" à l'expression trouvée :
en on a bien

Oui j'étais entrain de le faire c'est pourquoi je n'ai pas répondu plutôt, concernant votre question sur les aires, pour les moments il faut calculer les aire sous les courbes du diagramme effort tranchant.
Je vien de finir le moment fléchissant, je dois maintenant faire les équations de la question 4 avec les coupures, la route est longue haha.
Oui tu peux intégrer les équations obtenues pour l'effort tranchant, mais il faut faire attentions aux constantes d'intégration.
Raison pour laquelle je préfère utiliser la méthode semi-analytique proposée pour chaque tronçon, en faisant attention aux conditions aux limites.
C'est justement l'objet de la question 4 ...

Pour les équations de la méthode des coupures je coupe à chaque charge ponctuel
Si x compris entre 0 et 3 :
j'ai N(x)=0 kN V(x)= -Rby = -153,31 kN M(x)-153,31x donc M(x) = 153,31x
Si x compris entre 3 et 4 =
j'ai N(x)=0 V(x)+Rby-3 qui vaut V(x) = -153,31 + 3 = 150,31 kN
Je bloque pour la suite car je ne sais pas si je coupe avec x compris entre 4 et 6 car charge linéique(57,20 =péq)*8 vaut charge ponctuel au milieu de 8 mètre donc à 4 mètre.
la méthode semi-analytique proposée pour chaque tronçon, j'aimerais bien connaitre cette méthode.
Il faut que tu te concentres, je te l'ai expliquée dans mon message du 03-05-20 à 09:21, en te faisant le dernier tronçon.
Essaie de l'appliquer sur les autres tronçons en t'aidant de schémas, ça sera moins bancal que ta proposition de 13h18 où il manque le moment généré par la charge linéique ...

Mais du coup la prochaine équation sa serait à gauche en fonction de votre coupure fictive ou il faut faire une nouvelle coupure fictive ?
Il faut faire une coupure fictive sur chaque tronçon :
1) x  [0 ; c]
[0 ; c]
2) x  [c ; 2c]
[c ; 2c]
3) x  [2c ; 2c+e] => déjà fait, message du 03-05-20 à 09:21
[2c ; 2c+e] => déjà fait, message du 03-05-20 à 09:21
En vertu de la définition du torseur de cohésion, il faut regarder ce qu'il se passe soit à gauche de la coupure, soit à droite, le but étant de se simplifier la vie.
Je te joins un rappel succinct du cours que j'avais pu faire à un membre par le passé :
En gros, pour tracer les diagrammes des efforts pour une poutre soumise à un effort concentré et/ou à un champ linéique, on imagine qu'une section droite S de centre de gravité G et d'abscisse x (repère défini) établit une coupure fictive en x de la poutre :
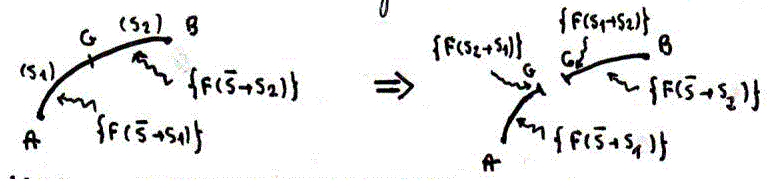
Par définition, le torseur de cohésion (ou torseur des efforts intérieurs) s'écrit :
Si tu appliques le principe fondamental de la statique, on démontre que ce torseur des efforts intérieurs peut s'écrire en un torseur des efforts extérieurs appliqués à la section
Voilà pourquoi tu peux analyser une poutre à gauche ou à droite de la section droite d'abscisse x (au signe près) pour tracer des diagrammes d'efforts intérieurs ou encore pour calculer ce torseur.
Faudrait peut-être pas trop traîner avec l'expression du moment fléchissant sur ces deux derniers tronçons pour passer au dimensionnement de cette poutrelle.

Effectivement je suis passé au dimensionnement des poteaux j'ai laissé faire mon binome le dimensionnement des poutrelles voici les question :
Données :
On choisira des poteaux de catégorie HE en acier S235.
Pour un poteau HE en acier S235, la résistance à la compression est de 235 MPa.
Module de Young E = 210 000 MPa
Question 9 =
Les réactions d'appui calculées à l'ELU à la question 3, correspondent aux forces de réaction des poteaux sur la poutrelle. Selon le principe des actions réciproques, déterminer les efforts normaux à l'ELU exercés en tête de chaque poteau (Nu1 pour le poteau 1 et Nu2 pour le poteau 2).
Afin de prendre en compte le poids propre des poteaux, on majore de 10% Nu1 et Nu2 : N'u1 = 1,1 Nu1 et N'u2 = 1,1 Nu2. Préciser les valeurs N'u1 et N'u2.
J'ai Rby et Rdy qui sont les réactions d'appuis dont on parle alors d'après la 3ème loi de Newton Rby exerce une force dans le sens inverse ainsi que Rdy car on nous précise : "Selon le principe des actions réciproques".
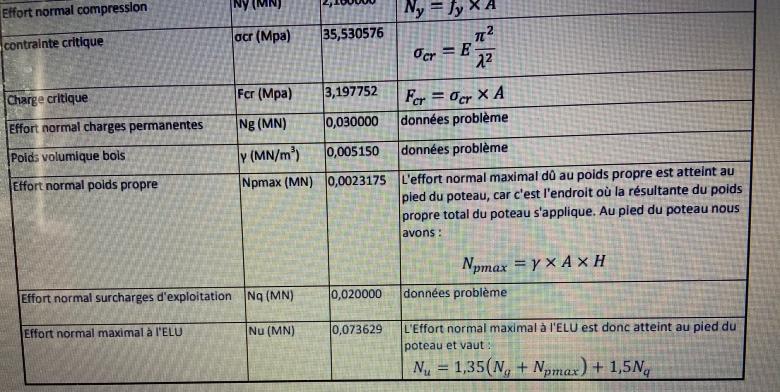
Nu = L'effort normal maximal à l'ELU est donc atteint au pied du poteau.
Sinon cela devrait être : Nu1 = -153,31 kN et Nu2 = -309,45 kN si l'on applique exactement la 3ème loi de Newton mais j'hésite car c'est négative.
Effectivement je suis passé au dimensionnement des poteaux j'ai laissé faire mon binome le dimensionnement des poutrelles voici les question : du coup c'est bon ? Les expressions des moments fléchissants sont cohérentes entre chaque tronçon de la poutrelle ?
Données :
On choisira des poteaux de catégorie HE en acier S235.
Pour un poteau HE en acier S235, la résistance à la compression est de 235 MPa.
Module de Young E = 210 000 MPa
(questions 5 à 9 non fournies ...)
Question 9 =
Les réactions d'appui calculées à l'ELU à la question 3, correspondent aux forces de réaction des poteaux sur la poutrelle. Selon le principe des actions réciproques, déterminer les efforts normaux à l'ELU exercés en tête de chaque poteau (Nu1 pour le poteau 1 et Nu2 pour le poteau 2).
Afin de prendre en compte le poids propre des poteaux, on majore de 10% Nu1 et Nu2 : N'u1 = 1,1 Nu1 et N'u2 = 1,1 Nu2. Préciser les valeurs N'u1 et N'u2.
Alors vu que Rby = 153,31 kN et Rdy = 309,45 kN alors Nu1 = 1/153,31 MN et Nu2 = 1/309,45 MN ?
Qu'est-ce que ce "MN" qui traîne ? Sinon c'est complètement faux, je préfère effectivement ceci (en admettant les valeurs trouvées pour les efforts aux appuis) :
Sinon cela devrait être : Nu1 = -153,31 kN et Nu2 = -309,45 kN si l'on applique exactement la 3ème loi de Newton mais j'hésite car c'est négative.
Pour toi que signifie ce signe négatif ?
On nous précise les efforts normaux à l'ELU exercés en tête de chaque poteau effectivment ils peuvent être négatif mais quand c'est négatif j'essaie toujours de m'assurer que c'est pas faux.
Voici d'où vien mon MN.
Sinon cela devrait être : Nu1 = -153,31 kN et Nu2 = -309,45 kN donc comme vous avez confirmer je continue avec ces réponses.
On nous précise les efforts normaux à l'ELU exercés en tête de chaque poteau effectivment ils peuvent être négatif mais quand c'est négatif j'essaie toujours de m'assurer que c'est pas faux.
Voici d'où vien mon MN.
J'ai compris ce que signifiait "MN", ce que je voulais te signifier c'est que ce n'est pas acceptable physiquement : si Rby ou Rdy sont en kN, 1/Rby ou 1/Rdy n'auraient jamais pu donner des MN. Attention donc à reprendre des unités, elles doivent être adaptées au contexte.
Concernant le principe des actions réciproques, si Rby et Rdy sont orientées vers le haut, cela signifie que leur composante suivant y sera positive.
Et donc les efforts sur les poteaux seront dans le sens contraire, d'où le signe négatif

Parfait, passant à la question 10 : On étudie le poteau 1. Préciser sa longueur de flambement. Déterminez l'inertie minimum Imin, afin que N'u1 soit inférieure à la charge critique de flambement : N'u1 inférieur à Pcr. Attention, le phénomène de flambement apparait suivant l'axe pour lequel l'inertie de la section est la plus faible.
Déterminer la section minimale Smin du poteau 1, afin que la contrainte normale Q'u1, liée à l'effort normal N'u1 soit inférieure à 235 MPa. Dimensionner le poteau 1 en prenant en compte ces 2 conditions (Smin et Imin).
Pour un poteau bi-articulé la longueur de flambement vaut la hauteur du poteau qui est ici b = 3 m
Comme j'ai déjà pu t'en faire part plus haut, je n'ai pas l'énoncé entre les questions 5 et 9 et n'ai pas les résultats de l'analyse de ton binôme, ça devient donc de plus en plus difficile de suivre votre état d'avancement réel sur le projet.
Concernant cette question 10, tu as un effort normal qui s'applique sur une poutre, tu peux donc appliquer la définition de la contrainte normale
avec S section de la poutre.
Tu peux en déduire une section permettant de respecter le critère de résistance à la compression (attention à prendre un coefficient de sécurité vis-à-vis de 235 MPa).
Il y a également la condition de flambement à vérifier vis-à-vis de l'inertie de la poutre => j'imagine que tu as eu un cours dessus ?
Je vien de trouver une hypothèse je sais pas si elle est vrai, dans le plan perpendiculaire à l l'axe zz' autour duquel se produit la flexion est l'axe de moment d'inertie minimum de la section droite.
Alors d'après moi Imin = 3/2 = 0.5 m^4 ?
Là il faut clairement que tu ouvres ton cours sur le flambement et que tu vérifies les conditions usuelles.
Il y a la théorie d'Euler qui pourrait te permettre d'avoir une expression pour la charge critique avec un coefficient qui dépend des types de liaisons : ici c'est articulé - articulé
avec l = b = 3 m ici
Mon binome vien de m'envoyer :pour la question 6 " j'ai compris ce qu'il faut calculer mais apparement il faut calculer les contraintes dans les semelles par rapport à l'épaisseur des semelles et faire la même chose pour l'âme".
Pour la question 7 : "je n'ai pas compris ce qu'il faut faire".
Question 5 : je ne referai pas les calculs, n'ayant pas tous les éléments à disposition.
Ce faisant, je suis surpris que vous ne teniez compte que de la contrainte de cisaillement et non de la contrainte normale due au moment fléchissant.
Question 6 : cela confirme d'autant plus ma remarque d'avant => j'ai l'impression que la vérification faite par ton binôme sur la contrainte de cisaillement pour la question 5 répondrait davantage à la question 6 ...
Question 7 : vous avez de la chance, l'équation de la déformée vous est fournie sur deux tronçons.
Pour donner l'allure, il suffit d'étudier la fonction v(x), comme vous l'auriez fait en maths.
La flèche correspond à un maximum pour la fonction => étude similaire à une fonction en maths.
D'accord à demain gbm  .
.
Je vous met ce que j'ai trouvé dans le cours concernant la question 10 j'ai trouvé une formule qui pourrait m'aider :
contrainte critique =(EI/A)*(pi/L)^2 = force critique/la section
ou contrainte critique = E*(pi^2/elancement mécanique^2.
Enfaite je ne comprends pas exactement la question 10 faut-il calculer l'inertie ou la contrainte critique ou la charge critique.
Bonjour,
Oui, cela s'apparente à la théorie d'Euler rappelée dans mon message du 03-05-20 à 19:48 avec pour une liaison articulée - articulée.
question 10 : On étudie le poteau 1. Préciser sa longueur de flambement. Déterminez l'inertie minimum Imin, afin que N'u1 soit inférieure à la charge critique de flambement : N'u1 inférieur à Pcr. Attention, le phénomène de flambement apparait suivant l'axe pour lequel l'inertie de la section est la plus faible => selon y
Etape 1 : étude de la résistance au flambement du poteau avec la charge critique, en exprimant une condition sur l'inertie
Déterminer la section minimale Smin du poteau 1, afin que la contrainte normale Q'u1, liée à l'effort normal N'u1 soit inférieure à 235 MPa. Dimensionner le poteau 1 en prenant en compte ces 2 conditions (Smin et Imin)
Etape 2 : étude classique à la compression, avec la formule rappelée dans mon message du 03-05-20 à 19:22
Pour un poteau bi-articulé la longueur de flambement vaut la hauteur du poteau qui est ici b = 3 m
Remarque importante : attention aux éventuels coefficients de sécurité à prendre en compte, suivant ce qui a été vu en cours.

A cause des imprévus je n'ai pas pu répondre plutôt, cependant je vous envoie les dernières questions du sujet qui est à finir avant 18h00 et à envoyer haha :
Question 11 : Répondre à la question 10 pour le poteau 2.
Question 12 : Les poteaux 1 et 2 sont maintenant dimensionnés. Déterminer le raccourcissement du poteau 1 dû à la force de compression N'u1. Déterminer le raccourcissement du poteau 2 dû à la force de compression N'u2.
Question 13 :
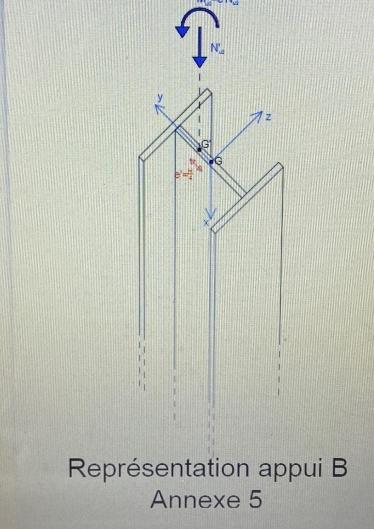
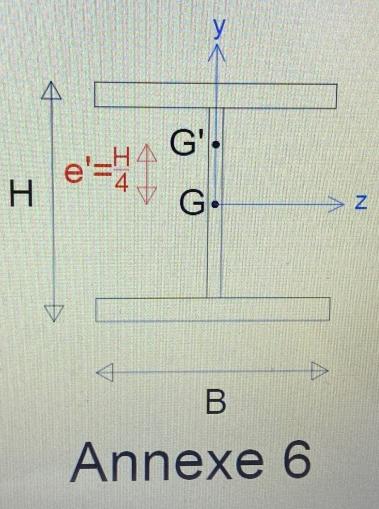
On suppose que pour le poteau 2, un défaut de conception entraine que le point d'application de la résultante N'u2 n'est pas en G, mais en G', situé à H/4 de G voir annexes 5 et 6. On appelle e' l'excentricité ( distance entre G et G') qui vaut donc e'=H/4.
L'execentricité génère un moment en tête de poteau de : e'N'u2.
Exprimer l'expression de la contrainte normale en tête du poteau 2 en fonction de e', N'u2, S2 (la section du poteau 2), Iz2 (l'inertie du poteau 2), et y. Faire l'application numérique : exprimer la contrainte normale uniquement en fonction de y. On se référera aux caractéristiques du poteau 2.
Question 14 :
Déterminer les valeurs des contraintes normales en fibre supérieure et en fibre inférieure. Analyser l'effet de l'excentricité. Tracer le diagramme des contraintes normales correspondantes en tête du poteau 2.
Je ne comprends pas ton raisonnement, on te demande d'exprimer une condition au flambement élastique pour déterminer l'inertie minimum "Imin" et miraculeusement tu me calcules une valeur de charge critique avec une valeur prise pour I ...
Méthode générale d'Euler avec L = b = 3 m ici et
et exprimer la condition

 ?
?
avec contrainte critique au flambement
contrainte admissible fournie par l'énoncé
coefficient de sécurité (en fonction du matériau de la poutre).
Il y a aussi a formule de Rankine mais je ne pense pas que tu l'aies vue en cours.
Ensuite, une fois que tu as déterminé Imin en exprimant la condition limite de flambement élastique, tu peux déterminer la section minimale via la formule rappelée dans mon message du 03-05-20 à 19:22.
Je télétravaille aujourd'hui, je vais donc être moins disponible que ces derniers jours :
---------------------------------------------------
Question 11 : Répondre à la question 10 pour le poteau 2.
--> même raisonnement que pour le poteau 1 en deux étapes.
Question 12 : Les poteaux 1 et 2 sont maintenant dimensionnés. Déterminer le raccourcissement du poteau 1 dû à la force de compression N'u1. Déterminer le raccourcissement du poteau 2 dû à la force de compression N'u2.
---> formule vue en classe (de mémoire )
Question 13 :
On suppose que pour le poteau 2, un défaut de conception entraine que le point d'application de la résultante N'u2 n'est pas en G, mais en G', situé à H/4 de G voir annexes 5 et 6. On appelle e' l'excentricité ( distance entre G et G') qui vaut donc e'=H/4.
L?excentricité génère un moment en tête de poteau de : e'N'u2.
Exprimer l'expression de la contrainte normale en tête du poteau 2 en fonction de e', N'u2, S2 (la section du poteau 2), Iz2 (l'inertie du poteau 2), et y. Faire l'application numérique : exprimer la contrainte normale uniquement en fonction de y. On se référera aux caractéristiques du poteau 2.
---> exploiter l'expression .y, y étant la cote de la fible considérée
Question 14 :
Déterminer les valeurs des contraintes normales en fibre supérieure et en fibre inférieure. Analyser l'effet de l'excentricité. Tracer le diagramme des contraintes normales correspondantes en tête du poteau 2
--> étude de l'expression trouvée en question 13
---------------------------------------------------
Bon courage pour la suite
Pour la question 10 je dois apparement utilisé cette formule pour connaitre la section « A » puis trouver l'inertie minimale sauf qu'il faut utiliser l'Arcelor Mittal pour trouver l'inertie Iz pour resoudre mon equation ci-dessous mais je ne le trouve pas.
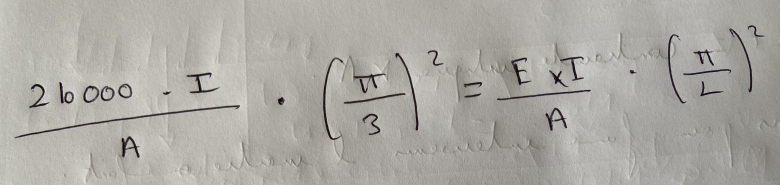
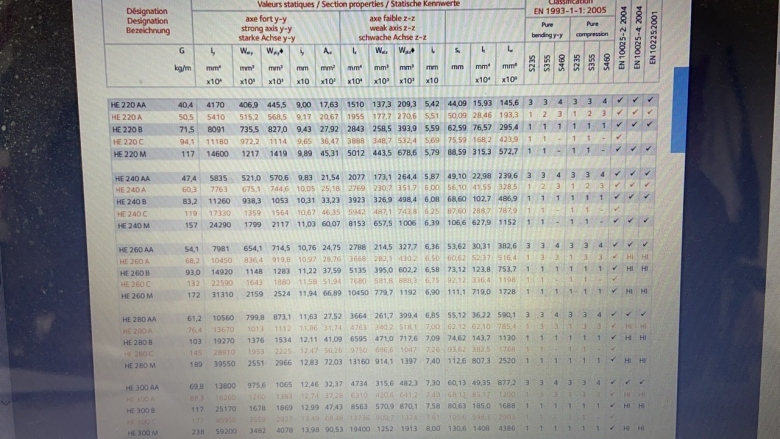
Je suis désolé, je n'applique pas des formules que je ne connais ou ne comprends pas (tu n'as pas l'air davantage convaincu avec ton "apparemment").
Pourquoi ne souhaites-tu pas appliquer ceci :
Données :
On choisira des poteaux de catégorie HE en acier S235.
Pour un poteau HE en acier S235, la résistance à la compression est de 235 MPa.
Module de Young E = 210 000 MPa
donc
C'est de l'acier, donc le coefficient de sécurité est
On cherche l'inertie minimale requise pour respecter la condition limite de flambement élastique :
Pour cela on va utiliser la méthode générale d'Euler que tu sembles avoir vue en classe :
avec
et exprimer la condition :
avec
Ou alors il y a la formule de Rankine mais ne sachant pas ce que tu as vu en cours, il faut que tu appliques celle que tu connais.

C'est bon gbm j'ai dû envoyé mes travaux au prof de rdm, sur ce merci pour vos aides qui m'ont aidés à faire beaucoup d'exercices mais surtout de les comprendre même si j'ai pas toujours été efficace haha.
Je recommenderai votre forum qui est très compétente.
Je reviendrai vers vous seulement l'année prochaine si j'ai des difficultés.
Je vous remercie de votre bienfaisance et vous souhaite une bonne journée et bonne continuation. 
Bonsoir rotu,
Désolé de ne pas avoir pu être aussi présent aujourd'hui, j'ai malgré tout essayé de t'aiguiller du mieux que je pouvais, sachant que c'est toujours difficile de refaire en quelques lignes un cours qui tient sur un polycopié de plusieurs pages.
J'espère malgré tout que notre échange sur ce projet t'aura permis de comprendre les fondamentaux de la RDM, de la rigueur à avoir dans la modélisation du problème, la définition des notations employées, de la qualité rédactionnelle à opérer, etc.
Les méthodes qu'on a vues ensemble te feront gagner du temps (notamment la méthode semi-analytique pour trouver plus rapidement un effort tranchant ou un moment fléchissant dans des cas simples).
Merci pour tes recommandations et tes encouragements, nous verrons bien si je suis encore en mesure de t'aider l'année prochaine (mes connaissances sur le sujet remontent il y a plus de 10 ans, j'oublie peu à peu) 
N'hésite pas à nous laisser un petit mot sur le livre d'or du site, ça fait toujours plaisir.
Bonne continuation et à bientôt !