Inscription / Connexion Nouveau Sujet
Projection d'un vecteur : utilisation de la base cartésienne.
Bonjour à tous,
Étant scolarisé à distance, je souhaiterais obtenir quelques avi sur la qualité de mon travail. Je posterai donc régulièrement des exercices réalisés et voici le premier :
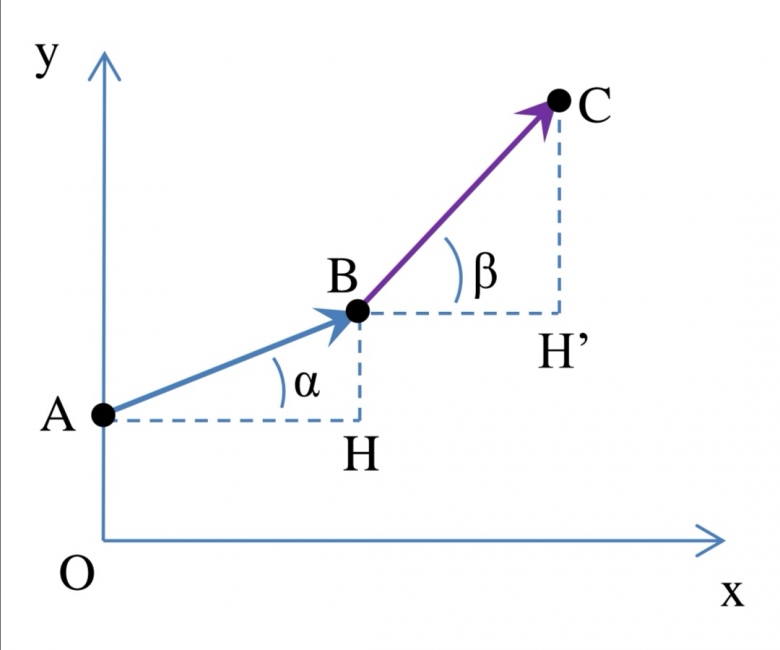
Dans le repère orthonormé direct R(0,ex,ey,ez) on considère les vecteurs AB et BC appartenant au plan (x0y) et tels que :
||AB||=1, ||BC||=sqrt(3),  =(ex, AB) =
=(ex, AB) = /6,
/6,  =(ey, BC) =
=(ey, BC) = /3 ( voir schéma)
/3 ( voir schéma)
1- en utilisant le triangle rectangle ABH calculer les projections orthogonales de AB su 0x et 0y. En déduire les coordonnées de AB
AB= (sqrt(3)) /2 ex+ (ay+ 0.5) ey
AB(sqrt(3)/2; 1/2)
2-meme chose pour le vecteur BC a l'aide du triangle BCH.
BC( sqrt(3)/2;3/2)
BC =sqrt(3)ex + (ay +2)ey
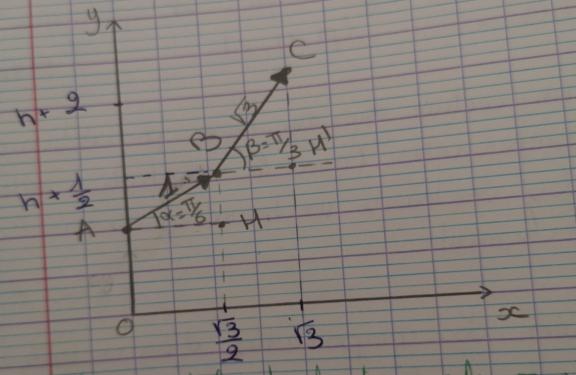
3-sachant que A(0,1,0) déterminer les position de B et de C
A(0,1,0)
B(sqrt(3)/2, 3/2,0)
C(sqrt(3), 3,0) ( voir photo 2)
4- déterminer les composantes cartésienne de AC et déduire celle du vecteur unitaire eac
AC= sqrt(3)ex+3ey
|| AC || =sqrt(12)= 2sqrt(3)
eac =AC/||AC||= 1/2 ex+ sqrt(3)/2 ey
Merci d'avoir pris le temps de me lire, je vous souhaite à tous une bonne journée