Bonjour Quinou,

c'est un exercice sur la relation entre objet et image donnée par un dioptre plan : il te faut donc connaître cette relation. Ci-dessous je te donne deux images issues de mon cours d'optique, j'espère qu'elle seront lisibles.
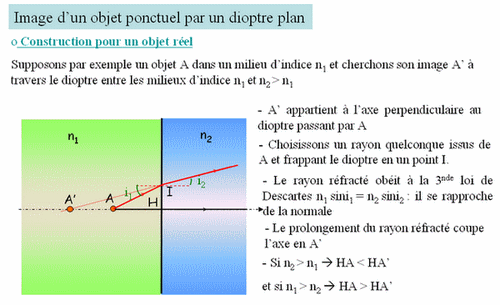
Sinon je te rappelle cette relation : soit un dioptre plan séparant deux milieux d'indices de réfraction n1 et n2 ; lorsqu'un objet A₁ placé à la distance HA₁ de ce dioptre (H est sur la surface de séparation) envoie des rayons faiblements inclinés (approximation de Gauss), alors le dioptre en donne une image A₂ telle que HA₁/n₁ = HA₂/n₂.
Dans cette relation HA1 et HA2 sont algébriques (il faudrait mettre une barre dessus... trop long).

Cette relation montre que HA1 et HA2 sont de même signe puisque n1 et n2 sont > 0. Donc à un objet A₁ réel correspond une image A₂ virtuelle, et vice-versa.

Cette relation conduit à HA₂ = HA₁.n₂/n₁.
1er cas : le pécheur regarde le poisson :

L'objet A1 est le poisson donc : HA₁ = 1 m,  n₁ = 4/3 ( le poisson est dans l'eau) et n₂ = 1.
Le calcul donne HA₂ = HA₁/n₁ + 0,75 m : l'image du poisson, captée par l'oeil du pêcheur, est bien rapprochée du dioptre.
Si on admet que la distance entre l'oeil du pêcheur est 1,7 m, le pécheur croit voir le poisson à la distance 1,7 + 0,75 =2,45 m, alors qu'il se trouve en réalité à 1,7 + 1 = 2,7 m.

ok ? Alors tu devrais faire le 2ième cas tout seul : cette fois l'objet A₁ est le pêcheur (HA₁ = 1,75 m), l'indice n₁ vaut 1 et n₂ vaut 4/3.

Je te laisse terminer.

petit erratum : Si on admet que la distance entre l'oeil du pêcheur et la surface du bassin est 1,7 m...

Oui donc si on veut être précis il faudrait enlever environ 10 cm. J'ai compris le calcul mais je me demandais si cette formule marchais aussi dans le cas ou un homme regarde verticalement le poisson

Et vous dites qu'il se trouve en réalité à 2.7 m  alors que dans l'énoncé c'est 1m

"si on veut être précis"... la distance réelle pêcheur-poisson est 2,7 m, tandis que la distance apparente est 2,45 m : la différence fait plus que 10 cm...

"si cette formule marchais aussi dans le cas ou un homme regarde verticalement le poisson " : la relation que je t'ai rappelée est réversible : si tu décides que A₂ est l'objet et A₁ l'image, il suffit d'adapter les indices pour obtenir cette image :

2ième cas, le poisson regarde le pécheur :

cette fois l'objet est le pécheur et le poisson regarde son image à travers le dioptre plan qui fait passer de l'air à l'eau.
Donc : HA₁ = 1,7 m, n₁ = 1, n₂ = 4/3. On obtient HA2 = 1,7 x 4/3 soit 2,27 m ; la distance entre le poisson et l'image du pécheur est alors 3,97 m (pratiquement 4 m).

Le pécheur voit le poisson plus près qu'il n'est en réalité (constatation familière ! regarde la bonde d'évacuation d'une baignoire remplie d'eau par exemple) ; le poisson voit le pécheur plus loin qu'il n'est en réalité...

"Et vous dites qu'il se trouve en réalité à 2.7 m  alors que dans l'énoncé c'est 1m" : qui ça, il ? il faudrait apprendre, en plus du cours, à être précis...

La distance exacte entre le pécheur est bien 1,7 m + 1 m = 2,7 m : c'est ce qu'on obtiendrait s'il n'y avait pas d'eau dans le bassin. Mais lorsque le bassin est rempli, le pécheur ne voit pas le poisson : il voit son image, qui elle se trouve à 0,75 m de la surface de l'eau. La distance apparente, pour le pécheur qui regarde le poisson, est donc 1,7 m + 0,75 m soit 2,45 m...

OK j'ai compris, mais dans ce même exercice on me demande ensuite a quelle profondeur semble se situer le poisson si l'observateur ne le regarde plus verticalement  ( sous un angle i ) est ce que je dois utiliser la même formule ?

Ah ça c'est différent : la relation que j'ai utilisée ci-dessus n'est applicable que pour des angles d'incidence petits (inférieurs à 15 degrés), que ce soir de l'au vers l'air ou de l'air vers l'eau.
Pour des angles plus grands (donc avec des rayons très obliques) elle n'est plus vraie, et l'image qu'on voit d'un objet à travers le dioptre plan présente des distorsions (un carré n'est plus un carré par exemple).

Le mieux est que tu consultes ce site : (clique sur la maison et tu y vas direct). Il s'agit d'une simulation ce ce que voit un poisson lorsqu'il regarde une figure triangulaire placée dans l'air. Une fois l'animation lancée, il faut faire un clic gauche sue le centre du rectangle, maintenir la touche enfoncée et déplacer la souris : tu verras les déformations subies par l'image du rectangle...

NB, tu auras besoin d'avoir la plate-forme Java installée sur ton ordi pour accéder à cette applet. Si ça ne marche pas dis-le moi, je ferai des captures d'écran et je te les enverrai.

BB.

Je veut bien des captures d'écran car ça ne marche pas, merci!

OK ; j'arrive dans 5 mn.

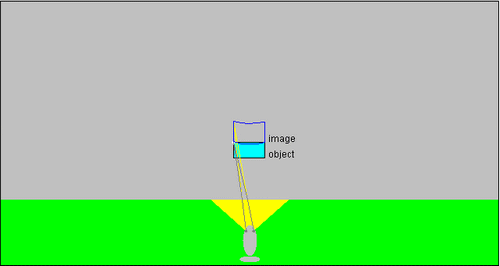
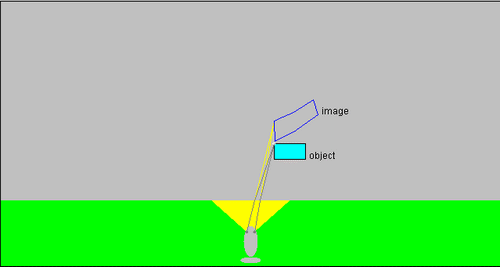
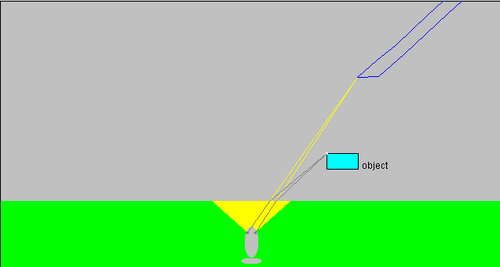
en voici quatre, en plaçant l'objet rectangulaire d'abord à la verticale au-dessus du poisson puis en augmentant l'oblicité des rayons.  BB.

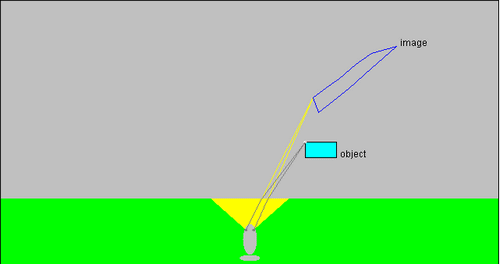
j'avais oublié qu'on ne pouvait pas mettre plus de 3 images dans un même post... voici donc la dernière.

Il faut préciser que si c'est un humain qui regarde un objet placé dans l'eau, les déformations sont moins importantes (car l'image de cet objet est rapprochée de la surface), et de plus le cerveau humain "rectifie" la forme de cet objet en fonction de sa propre bibliothèque d'images (quand on "sait" qu'on doit voir un rectangle, on a tendance à en voir un...). Ce phénomène d'interprétation des images perçues est évidemment perfectible et conduit à de nombreuses illusions d'optique.

pour le poisson, je ne sais pas.

A bientôt si tu as encore des problèmes en optique.  BB.

Merci pour toute vos explications, bonne soirée!

Bon courage pour la suite de tes études, et à bientôt peut-être  .  BB.