Bonjour john35,

Tu n'as pas besoin d'avoir une bonne vision dans l'espace. Je peux te donner ma méthode qui est analogue à la règle des 3 doigts mais qui ne nécessite pas de poser son stylo.

On a deux vecteurs a et b quelconques et on veut donc calculer a^b. Tu regardes l'angle . Si alors a^b vient vers nous. Si , a^b nous fuit (on prend alpha positif ie non algébrisé). Tu peux t'en persuader avec quelques exemples.

Younes1.

merci mais par exemple ( voir image en pièce  jointe) comment faire si on a un cube ABCDEFGH et que l'on doit trouver
AE vectoriel EH,là ça ne fonctionne pas ta méthode à moins que j'ai mal compris.

merci d'avance

Cordialement

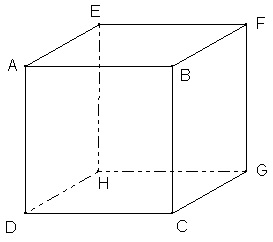
AE^EH=(-EA)^EH=-EF (si c'est des vecteurs unitaires). Et pour le calculer tu appliques ma méthode à EA^EH. Tu as (EA,EH)=90° (sens trigo) et donc le produit vectoriel vient vers nous ( quand on est dans le plan (AEH) ). Sinon pour aller plus vite et ne pas t'embêter, tu "translate" AE tel que A coincide avec E ( tu t'imagines AE sortant du cube vers la droite quand tu est dans (AEH) ) et là t'appliques ma méthode à et l'angle entre AE et EH est de +270° (sens trigo). Si tu veux j'avais oublier de préciser qu'il fallait faire "coincider" les origines des vecteurs.
Je ne sais pas si c'est clair.

mais vecteur EF est vers la droite il est pas fuyant je comprends pas .tu peux me ré expliquer stp?

Oui mais cela dépend d'où tu l'observes. Places toi dans le plan (EAH) c'est à dire que tu t'imagines regarder le carré EADH. Alors quand tu es face à lui EF vient vers toi. Donc -EF te fuit. Donc dans le plan (EAH), EA^EH = +EF (règle des trois doigts-ma méthode). Donc AE^EH = (-EA)^(EH) = -(EA^EH) = -EF.

Si j'ai bien compris par exemple AE vectoriel EF =EH  et  AB vectoriel  BF= BC est ce correct ?

Oui pour le premier et non pour le deuxième, le résultat est CB : tu translates AB (dans le plan (ABF)) de sorte à ce que A coincide avec B. L'angle entre AB et BF est alors de + pi/2 (toujours sens trigo) donc le produit vectoriel est selon CB : il vient vers toi quand tu regardes la face ABFE "d'en haut".

est ce que AE vectoriel EF= -EH est ce exact ?

Oui c'est exact.

un petit dernier pour voir si j'ai bien compris

AH vectoriel AE=AF est ce correct?

Je crois m'etre trompé Ça ne serait pas AB plutôt ? ) est ce exact?

Non je pense que c'est AB  je demande juste confirmation

Personne ?

mais ta méthode ne fonctionne pas si je prends par exemple AG vectoriel AE?  Comment faire?

en fait j'ai un problème de visualisation dans l'espace du produit vectoriel et plus particulièrement dans les trièdres .je connais toutes les règles mais j'arrive pas à visualiser.il y aurait pas une méthode miracle assez accessible. le produit vectoriel devient mon cauchemard !!!

Oui c'est AB pour ton premier et si ma méthode marche et pour AG ^ AE il faut juste "visualiser" la bonne face : c'est ACGE, le vecteur AG ^ AE est donc orthogonal à (ACG) et sort en haut à droite c'est donc HF.

mais comment sait on que c'est la face  ACGE  ? Je ne comprends pas.peux tu me réexpliquer stp.