Inscription / Connexion Nouveau Sujet
probleme travail des frottements
bonjour je bloque juste sur cette question d'un exo, pourriez vous m'aider svp
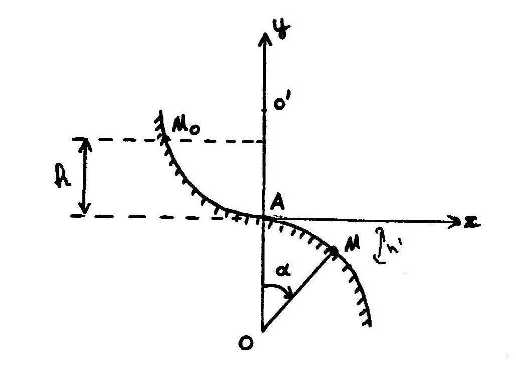
on considère un point M de masse m assujetti à se déplacer dans le plan vertilcal Axy, sur des surfaces cylindriques d'axe parallèle à Az de centres respetifs O et O' de même rayon R.
Le point M initialement en Mo est lâché sans vitesse initiale à uen hauteur h au dessus de Ax. On note g le module de pezsanteur .
Le point M quitte la surface à une hauteur h' au dessous de Ax
Je dois trouver le travail de la force de frottemenbt en focntion de m ,g, h ,h' pour comparer h et h'.
je m'étais dit : il faut appliquer théoreme de l'énergie mécanique :
Variation de l'énergie méca = travail force Frottement
1/2 mv² - mgh' - mgh = travai frottement ...
mais je sens que il faudrait qu'il y ait + mgh' ou qqch du genre et de toute façon je suis bloqué avec le v ... comment faire svp? Merci d'avance pour votre aide.
Au point où M quitte le "toboggan", si la masse était posée à l'arrêt à cet endroit, la réaction normale à la surface du toboggan due au poids de la masse serait N = P.cos(alpha).
Du fait de sa vitesse, au passage en ce point, la masse subit une force centrifuge F = m.v²/r (en se plaçant dans le référentiel de la bille, si on est dans un autre référentiel, par exemple galiléen, on n'utilise pas la notion de force centrifuge, mais cela revient au même)
La masse ponctuelle quitte la piste au point au la somme de |N| = |F|
--> P.cos(alpha) = m.v²/r
mg.cos(alpha) = m.v²/r
g.cos(alpha) = v²/r (1)
-----
Le travail du poids enre les 2 positions extrème est mg(h+h')
Soit W le travail des forces de frottement entre ces 2 points.
Le travail utile est donc: mg(h+h') - W
C'est celui-ci qui se transforme en énergie cinétique et donc au point bas, on a:
(1/2).m.v² = mg(h+h') - W
v² = 2g(h+h') - 2W/m
(1) -->
g.cos(alpha) = [2g(h+h') - 2W/m]/r (2)
On a : h' = r - r.cos(alpha)
cos(alpha) = (r-h')/r
(2) -->
g.(r-h')/r = [2g(h+h') - 2W/m]/r
g.(r-h') = 2g(h+h') - 2W/m
gr - gh' = 2gh + 2gh' - 2W/m
2W/m = 2gh + 3gh' - gr
W = (1/2).gm.(2h + 3h' - r)
-----
Sauf distraction ou erreur. 
eu merci beaucoup mais etait -il n'écessaire d'introduire h? parce que l'énoncé stipulait bien qu'il fallait uniquement ecprimer ce travail en fonction de h, h', m et g ... merci bcp d'avance
(et aussi que je ne connais absolument pas la force centrifuge donc la partie (1) de votre explication est floue pour moi 
non en fait pardon je reprends ma question , j'ai tout compris sauf l'égalité 1 (normal je ne connais que le PFD et le théoreme de l'énergie cinétique / mécanique) pourriez vous m'aider?
non en fait encore plus simple moi je comprends pas pourquoi vous avez écrit :
mg(h+h') - W = 1/2mv²
Moi en faisant : la variation de l'énergie mécanique est égale a la somme dees forces non conservatives j'obtiens:
1/2mv² - mg(h+h') = + W et non pas - ... d'où viendrait alors mon erruer? 
Tout est convention de signe.
Je ne sais pas quelles conventions tu utilises.
Pour moi, un travail est pris en valeur absolue et j'ajoute un signe en fonction qu'il est consommateur ou producteur d'energie.
Pour toi, le signe est lié au travail.
Utilise les conventions qu'on t'a apprises et mets un - si tu veux, cela revient au même tant qu'on sait les conventions de signe qu'on utilise.



