Excusez-moi .. Je peux bien recopier l'énoncé mais je ne sais pas faire de circuit à part en paint ce qui rend les choses assez moches. Si vous avez une suggestion, je suis preneuse.

Bonjour,

Il est très facile de faire une copie d'écran de l'image et de la poster.

Pour information : je trouve i₃ 0,636 3... A que l'on peut arrondir à 0,64 A

Note : un résultat numérique sans son unité ne veut strictement rien dire.

Pour savoir d'où provient ton erreur, il faut que tu postes tes calculs.

Difficile à dire sans l'énoncé mais, apparemment, le théorème de superposition semble imposé. Sinon, le théorème du "potentiel de nœud" souvent appelé théorème de Millman, donne directement le potentiel du nœud commun aux trois résistances. Ensuite, la loi d'Ohm appliquée à chaque résistance permet la détermination des trois intensités. La méthode est plus rapide que celle utilisant le théorème de superposition sauf dans le cas particulier d'un montage "symétrique" : R1=R2 et E1=E2.
Mais si le théorème de Millmann n'est pas à son programme, que thadea oublie vite ce message !

Cela semble très fatigant de recopier un énoncé d'une phrase :

"En appliquant le théorème de superposition, calculer l'intensité i₃"
____________

Exercice de ...

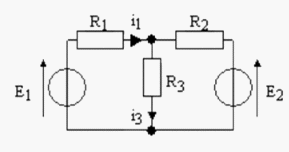
En notant la tension aux bornes de la loi d'Ohm permet d'écrire que :



1.) Par le théorème de superposition

Résistances en parallèle et en série ; pont diviseur de tension...

1.a.) Le générateur de droite étant remplacé par un court-circuit



Application numérique :

1.b.) Le générateur de gauche étant remplacé par un court-circuit



Application numérique :

1.c.) Superposition



2.) Par le théorème de Millman



Application numérique :

Ou par Equivalent Thévenin :

Avec R3 enlevé : Uth = E1 + (E2-R1)*R1/(R1+R2) = (E1.R2 + E2.R1)/(R1+R2)

Rth = R1 // R2 = R1R2/(R1+R2)

On arrive donc à un circuit équivalent :



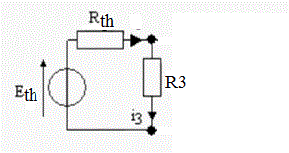
D'où on tire directement : i3 = Uth/(Rth + R3)

i3 = [(E1.R2 + E2.R1)/(R1+R2)]/(R3 + R1R2/(R1+R2)]

i3 = (E1.R2 + E2.R1)/(R1R2 + R1R3 + R2R3)

... dont je ne peux pas calculer la valeur numérique, puisque celles de E1, E2 , R1, R2 et R3 ne sont pas données.

Bonjour J-P

Merci pour cet enrichissement. Pour ma part, j'aime beaucoup les quelques topics qui montrent ainsi qu'il y a de nombreuses méthodes pour obtenir (plus ou moins directement) la solution.

Les valeurs numériques :






Ton expression :

Salut Coll.

Bonsoir,
Puisqu'il est question de méthodes diverses pour étudier un même circuit, en voici une autre, pas tout à fait aussi rapide et générale que les applications des théorèmes de Millman, Thévenin ou Norton mais que les étudiants apprécient en général.
Il s'agit simplement de remplacer les générateurs linéaires de tension (générateurs de Thévenin) par les générateurs linéaires de courant équivalent (générateurs de Norton) et de regrouper les résistances.
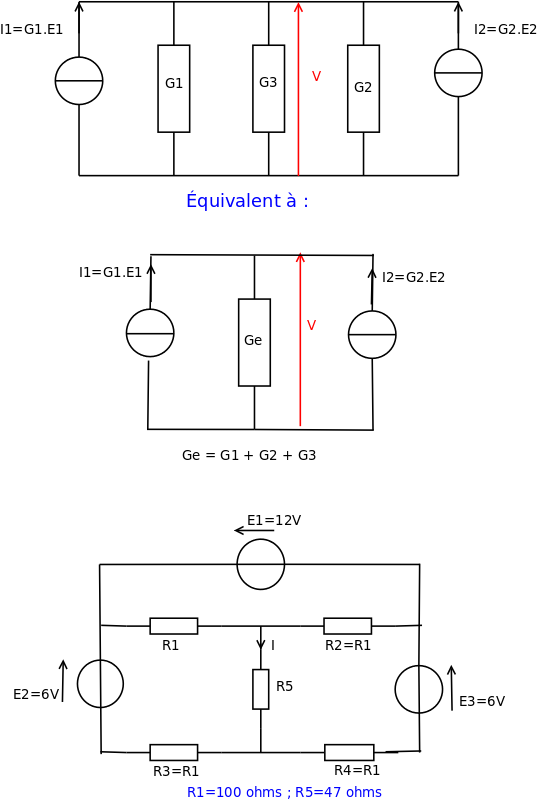
En notant G1, G2, G3 les conductances, on obtient les schémas équivalents ci-dessous . La loi d'Ohm appliquée à la conductance équivalente conduit immédiatement à :
.
Exactement le résultat obtenu directement à partir du théorème de Millman.
La loi d'Ohm appliquée au conducteur n°3 conduit au résultat final :
.
On peut revenir au résultat faisant intervenir les résistances en multipliant chacun des termes de l'expression précédente par le produit R1.R2.R3.
Chacun bien sûr a ses habitudes mais je ne crois pas que le théorème de superposition soit le plus approprié  pour ce montage. Je ne sais pas si cela va intéresser thadéa mais je propose un autre montage où le théorème de superposition est vraiment efficace pour déterminer l'intensité I traversant le conducteur de résistance R5.

Bonjour à tous,

Merci vanoise pour ce nouvel enrichissement.
Alors, puisque nous sommes dans les diverses méthodes... Une classique (mais certainement moins conseillée pour ce schéma) : mailles et n?ud...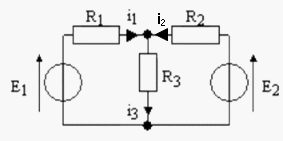





Le système à résoudre est donc :



Par exemple par la méthode de Gauss :







D'où i₃ 0,64 A

et si l'on est curieux de connaître aussi i₁ et i₂ :





D'où i₁ 0,45 A
et
i₂ 0,18 A

Merci Coll !
Je pense effectivement que les bonnes vieilles lois de Kirchhoff trouvent un regain d'intérêt pour les circuits compliqués maintenant que les ordinateurs et même les simples calculatrices sont capable de résoudre un système d'équations linéaires à plusieurs centaines d'inconnues.